Cell shape can mediate the spatial organization of the bacterial cytoskeleton

Abstract

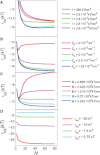
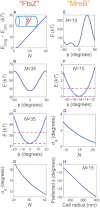
The bacterial cytoskeleton guides the synthesis of cell wall and thus regulates cell shape. Because spatial patterning of the bacterial cytoskeleton is critical to the proper control of cell shape, it is important to ask how the cytoskeleton spatially self-organizes in the first place. In this work, we develop a quantitative model to account for the various spatial patterns adopted by bacterial cytoskeletal proteins, especially the orientation and length of cytoskeletal filaments such as FtsZ and MreB in rod-shaped cells. We show that the combined mechanical energy of membrane bending, membrane pinning, and filament bending of a membrane-attached cytoskeletal filament can be sufficient to prescribe orientation, e.g., circumferential for FtsZ or helical for MreB, with the accuracy of orientation increasing with the length of the cytoskeletal filament. Moreover, the mechanical energy can compete with the chemical energy of cytoskeletal polymerization to regulate filament length. Notably, we predict a conformational transition with increasing polymer length from smoothly curved to end-bent polymers. Finally, the mechanical energy also results in a mutual attraction among polymers on the same membrane, which could facilitate tight polymer spacing or bundling. The predictions of the model can be verified through genetic, microscopic, and microfluidic approaches.

Figure 1

Bacterial cytoskeletal polymers. (A) Various orientations adopted by bacterial cytoskeleton components. (B) Schematic illustration of the polymer-membrane model.

Figure 2

Polymer-membrane energies and conformations. (A–D) Ground-state polymer bending energy (E_p), membrane energy (E_m), combined energy (E), and energy increment per monomer (ΔE) as functions of polymer length N (energies in units of the thermal energy kT). (E and F) Membrane and polymer conformations for polymers of length N = 9 and 19 oriented along the x axis. (G and H) Three-dimensional membrane conformations for polymers of length N = 9 and 19 from panels E and F. (Note expanded scale normal to the membrane.) Parameters are: membrane bending modulus K = 28 kT; membrane-pinning modulus λ = 0.28 kT/nm⁴; monomer diameter d = 4 nm; polymer bending modulus B = 6.07 × 10³kT⋅ nm; and polymer intrinsic curvature C₀ = 0.01 nm⁻¹.

Figure 3

Ground-state polymer length. (A) Total system energy per monomer ε_tot (including monomer-monomer interaction energy ε_int) as a function of polymer length N for various pinning moduli. The minimum of each curve is the global ground state. (B) ε_tot versus N for various polymer intrinsic curvatures. (C) ε_tot versus N for various polymer bending moduli. (D) ε_tot versus N for various monomer-monomer interaction energies. Parameters as in Fig. 2 with ε_int = −15 kT, except as indicated.

Figure 4

Polymer length for nonequilibrium growth conditions. (A) System free-energy increment ΔG for monomer addition versus polymer length N for different pinning moduli, with C₀ = 0.02 nm⁻¹. The point of intersection of each energy increment curve with ΔG = 0 (black line) indicates where polymer growth stops being energetically favorable. (B) ΔG versus N for various intrinsic polymer curvatures, with λ = 2.8 × 10⁻⁶kT/nm⁴. (C) ΔG versus N for various polymer bending moduli, with C₀ = 0.001 nm⁻¹. (D) ΔG versus N for various polymerization energies, with λ = 2.8 × 10⁻⁶kT/nm⁴. Parameters as in Fig. 2 with g_poly = −4.0 kT, except as indicated.

Figure 5

Preferred polymer orientation. (A) Energy difference between longitudinal (ϕ = 90°) and circumferential (ϕ = 0°) orientations as a function of length N for an FtsZ-like polymer, i.e., one with intrinsic curvature bigger than the circumferential curvature of the cell. (B) Energy versus FtsZ orientation for N = 35. (C) Blowup of panel B: thermal fluctuation of 1 kT (magenta lines) leads to an orientation fluctuation of <13°. (D) FtsZ orientation fluctuation (σ_ϕ) versus polymer length. (E) Energy versus orientation for an MreB-like polymer, i.e., one with polymer intrinsic curvature less than the circumferential curvature and with a preferred twist. (F) Blowup of panel E: thermal fluctuation of 1 kT (magenta lines) leads to an orientation fluctuation of <3°. (G) MreB orientation fluctuation versus polymer length. (H) Preferred MreB orientation versus cell radius. Parameters in panels A–D are the same as in Fig. 2, except C₀ = 1/R + 0.01 nm⁻¹, with R = 350 nm. Parameters in panels E–H are K = 28 kT, λ = 0.28 kT/nm⁴, d = 5.1 nm, B = 3.79 × 10⁶kT · nm, R = 400 nm, C₀ = 2.31 × 10⁻³ nm⁻¹, torsional rigidity of the polymer τ = 2.54 × 10⁶kT · nm, and polymer intrinsic twist per unit length ω₀ = −6.62 × 10⁻⁴ nm⁻¹.

Figure 6

Polymer-polymer interaction. (A) Schematic illustration of two well-separated FtsZ-like polymers and two adjacent FtsZ-like polymers. (B) Energy difference between the two configurations, E₀ for adjacent polymers and E_∞ for well-separated polymers, as a function of polymer length N. Parameters as in Fig. 2, except as indicated.