A mathematical model of forgetting and amnesia

Abstract

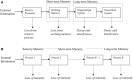
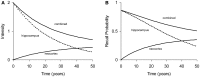
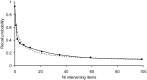
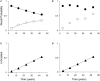
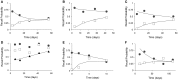
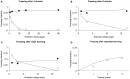
We describe a mathematical model of learning and memory and apply it to the dynamics of forgetting and amnesia. The model is based on the hypothesis that the neural systems involved in memory at different time scales share two fundamental properties: (1) representations in a store decline in strength (2) while trying to induce new representations in higher-level more permanent stores. This paper addresses several types of experimental and clinical phenomena: (i) the temporal gradient of retrograde amnesia (Ribot's Law), (ii) forgetting curves with and without anterograde amnesia, and (iii) learning and forgetting curves with impaired cortical plasticity. Results are in the form of closed-form expressions that are applied to studies with mice, rats, and monkeys. In order to analyze human data in a quantitative manner, we also derive a relative measure of retrograde amnesia that removes the effects of non-equal item difficulty for different time periods commonly found with clinical retrograde amnesia tests. Using these analytical tools, we review studies of temporal gradients in the memory of patients with Korsakoff's Disease, Alzheimer's Dementia, Huntington's Disease, and other disorders.

Keywords: Alzheimer’s disease; Korsakoff’s syndrome; amnesia; consolidation; cortex; forgetting; hippocampus; mathematical modeling.

Figure 1

Illustration of the memory chain. (A) Memory systems at different time scales, with memory decline in each system and induction (generation) of new representations in the next system. (B) Abstract representation used in the Memory Chain Model.

Figure 2

Example of typical forgetting curve with simulated underlying processes in hippocampal and neocortical stores. (A) Intensity as a function of time. (B) Recall probability as a function of time. The curves in (A,B) are based on the same parameters.

Figure 3

Example application of the Memory Chain Model to a forgetting curve, with a high number of observations per data point using a three-process recall probability function (solid curve) and the power-law (dotted curve). The recall data are word pairs from Rubin et al. (1999). Each data point is based on 1800 observations. The model fitted well on the chi-square test, which becomes more severe with the number of observations (α = 0.55 and R² > 0.999). The power-law was rejected by the chi-square test.

Figure 4

Illustration of partial retrograde amnesia, from a full lesion to no lesion of Process 1 (hippocampus/MTL). Values of the lesion parameter λ were 1.0, 0.875, 0.75, 0.5, and 0.0. The other parameters were μ₁ = 2.0, a₁ = 0.3, μ₂ = 0.1, and a₂ = 0 (simulated data with arbitrary time units).

Figure 5

The relative retrograde gradient remains unaffected by manipulation of item difficulty. (Illustration with self-generated data points. (A) Example forgetting curve (white dots) and Ribot gradient (black dots), generated with the model using μ₁ = 2, a₁ = 0.04, μ₂ = 0.01, and a₂ = 0. (B) Distorted curve where μ₁ has been multiplied with (from left to right) 1, 1.4, 1.8, 1.4, and 2. (C) Relative retrograde gradient for the undistorted curves. (D) Relative retrograde gradient for the distorted curves.

Figure 6

Data from three studies with Korsakoff patients and controls (Albert et al., ; see Studies a–c in our Table 3). In each study, panels 1 and 2 represent easy and hard items, respectively. Open circles represent patient data, solid circles controls. Panels 3 and 4 give the relative retrograde gradient for easy and hard items, respectively, shown with triangles. The solid curves are fits by the model, assuming that a₂ = 0.

Figure 7

Fits of the model to six animal experiments on retrograde amnesia. Experimental animals have lesions to various parts of the MTL (open squares), controls have mock lesions (closed circles). Fitted lines are solid without markers. See Table 2 for further details. (A) Using mice with two-choice spatial discrimination (Cho et al., 1993). (B) Using mice with two-choice spatial discrimination (Cho and Kesner, 1996). (C) Using rats in a contextual fear paradigm (Kim and Fanselow, 1992). (D) Using rats (Wiig et al., 1996). Here, the triangles represented the relative retrograde gradient, as in Figure 6. (E) Using rats with social learning of food preference (Winocur, 1990). (F) Using monkeys in a delayed matching to target task (Zola-Morgan and Squire, 1990).

Figure 8

Forgetting with various levels of anterograde amnesia caused by increasing lesion sizes in a DNMT task (Squire and Zola-Morgan, 1991). (A) Data (points) and model fit (solid lines). Performance as a function of delay period (logarithmic time scale). (B) Relative, functional lesion sizes in the medial temporal lobe (MTL), derived from the working-memory-to-MTL learning rates (see text). Here, 100% would be a full, functional lesion.

Figure 9

Observed freezing data (circles) and predicted data (lines) of the study by Frankland et al. (2001) using the assumption of zero consolidation in the experimental condition (see text). Open circles refer to experimental subjects (mice), closed circles to controls. (A) Forgetting curves after learning with three foot shocks. (B) Forgetting curves after learning with eight foot shocks. (C) Forgetting curves after learning with one foot shock (controls) and eight foot shocks (experimental). (D) Repeated learning in experimental animals receiving one foot shock per day. The observed data are averaged over two conditions (see text for details).

Figure 10

Ten studies with Korsakoff’s Disease patients and matched controls. The letters a–j with each panel correspond to Studies a–j in Table 3. The panels are presented in pairs, where panel 1 of a pair contains the measured data (solid circles are controls, open circles are patients), and 2 the data transformed to a relative retrograde gradient (always shown as triangles, with the solid line indicating the model fit).

Figure 11

Three studies with Alzheimer’s Dementia patients and matched controls. The letters with each panel correspond to those in Table 3. See Figure 10 for further explanation.

Figure 12

Four studies with Huntington’s Disease patients and matched controls. The letters with each panel correspond to those in Table 3. See Figure 10 for further explanation.

Figure 13

Seven studies with various patient groups and matched controls. The letters with each panel correspond to those in Table 3. See Figure 10 for further explanation.