Role of committed minorities in times of crisis

Abstract

The surprising social phenomena of the Arab Spring and the Occupy Wall Street movement posit the question of whether the active role of committed groups may produce political changes of significant importance. Under what conditions are the convictions of a minority going to dominate the future direction of a society? We address this question with the help of a Cooperative Decision Making model (CDMM) which has been shown to generate consensus through a phase-transition process. We observe that in a system of a finite size the global consensus state is not permanent and times of crisis occur when there is an ambiguity concerning a given social issue. The correlation function within the cooperative system becomes similarly extended as it is observed at criticality. This combination of independence (free will) and long-range correlation makes it possible for very small but committed minorities to produce substantial changes in social consensus.

Figure 1

(a–c) Temporal evolution of the global order parameter for increasing values of the control parameter, K = 1.50, K = 1.62 and K = 1.66. (d) Phase transition diagram for the amplitude of the global order parameter ξ(t) as a function of the control parameter K. (e) Survival probability distribution Ψ(τ) for selected values of K: blue line corresponds to K = 1.50, red line to K = 1.62 and green line to K = 1.66. Lattice size is N = 100 × 100 nodes, and transition rate g = 0.10; all the calculation were done with periodic boundary conditions.

Figure 2. Scaling properties of the CDMM.

(a) Global order parameter ξ_eq is evaluated as a function of the coupling constant for increasing size of the lattice and data collapse is observed for rescaled variables. (b) Scaling of the global order parameter in the vicinity of the phase transition point. (c) Correlation C(r) as a function of the Euclidean distance r between nodes of the lattice for K being K = 1.50 (blue line), 1.62 (red line) and 1.66 (green line), respectively. (d) Scaling of the susceptibility in the vicinity of the critical point. Critical control parameter K_c = 1.644, β = 1/8, γ = 7/4 and ν = 1. Lattice size is N = 100 × 100 nodes, transition rate g = 0.10.

Figure 3. Behaviour of the CDMM on a three-dimensional simple cubic lattice.

(a–c) Temporal evolution of the global order parameter for increasing values of the coupling constant, K = 1.00, K = 1.30 and K = 1.50, respectively. (d) Phase transition curves for the CDMM evaluated on the 3D lattice of size N = L³, for three sizes of the cube. (e) Survival probability function derived from the fluctuations of the global order parameter for increasing values of the coupling constant. Plots (a–c) and (e) refer to lattice of size L = 5, plot (d) to lattice of size L = 10 and for all simulations periodic boundary conditions were used, and g = 0.10.

Figure 4. Temporal evolution of the correlation function C(r,t).

On each panel color map encodes spatiotemporal variability of correlation C(r,t). The middle plot shows cross-section of this map for r₀ = 15 and bottom plot shows corresponding evolution of the global order parameter ξ(t). Analysis performed for K = 1.50 (a), K = 1.62 (b) and K = 1.66 (c). Lattice size is N = 100 × 100 nodes and transition rate g = 0.10.

Figure 5. Configuration of the lattice (a–c) and corresponding correlation function (bottom panel) for instances marked on bottom panel of Fig.4(c) by arrows.

White areas correspond to the units in state "yes" and black to the units in the state "no". Lattice size is N = 100 × 100, coupling constant is K = 1.66 and transition rate is g = 0.10.

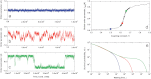
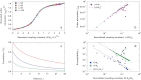
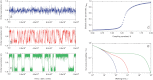
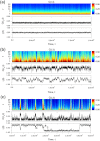
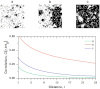
Figure 6. Temporal evolution for the global order parameter in the absence of the minority is compared with its evolution once a committed minority is present.

(Left) Fluctuations of the global variable ξ(t) for K = 1.65 and the 2D lattice of size N = 100 × 100 nodes are compared with the behaviour of ξ(t) once 1% of the randomly selected nodes are kept in state "yes" at all time. (Right) The dynamics of the CDMM on the 3D lattice when a 1% committed minority is present. The studied lattice has N = 5 × 5 × 5 nodes, thus 1 node was always kept in state “+1” to realize the committed minority concept. Coupling constant is K = 1.40. In both cases transition rate is g = 0.10. Time interval τ marked on the top left panel denotes one of the global majority states. Its duration becomes significantly extended once committed minority is present, as can be seen on the bottom left panel. The time interval τ_yes shows strong shift in the length of positive and negative majority states due to the presence of the minority.

Figure 7. (Left) Mean waiting time obtained for system with no acting minorities (blue dots) increases once 1% (red dots) and 5% (orange dots) committed minority is present.

(Right) The ensemble average of 1000 independent realizations of the CDMM initialized with a random configuration (blue line) is compared with those initialized with a crisis configuration (red curve). Dashed lines correspond to the average value of the ensemble average in the long time limit with one standard deviation of its fluctuations added and subtracted.