Coherent tunnelling across a quantum point contact in the quantum Hall regime

Abstract

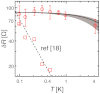
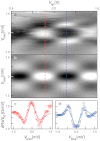
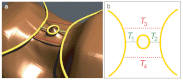
The unique properties of quantum hall devices arise from the ideal one-dimensional edge states that form in a two-dimensional electron system at high magnetic field. Tunnelling between edge states across a quantum point contact (QPC) has already revealed rich physics, like fractionally charged excitations, or chiral Luttinger liquid. Thanks to scanning gate microscopy, we show that a single QPC can turn into an interferometer for specific potential landscapes. Spectroscopy, magnetic field and temperature dependences of electron transport reveal a quantitatively consistent interferometric behavior of the studied QPC. To explain this unexpected behavior, we put forward a new model which relies on the presence of a quantum Hall island at the centre of the constriction as well as on different tunnelling paths surrounding the island, thereby creating a new type of interferometer. This work sets the ground for new device concepts based on coherent tunnelling.

Figure 1. Schematic representation of our model and experimental setup.

Tunnelling paths (dotted lines) connect opposite ES through aquantum Hall island (circle). Current-carrying contacts (1–2) and voltage probes (3–4) allow resistance measurements. (only one edge state is represented for the sake of clarity).

Figure 2. Imaging tunnelling across a QPC.

(a) SGM map at B = 9.5 T, T = 4.2 K, and V_tip = −4 V. Continuous lines correspond to the edges of the QPC. The black bar represents 1 µm. (b) B-dependence of R-profiles over the region marked with a dashed line in (a), with V_tip = −6 V. Using Eq. (1) for the two consecutive fringes highlighted with the white dashed lines in (b), we calculate in (c) the diameter of the QHI as the tip-QHI distance δ_x is varied.

Figure 3. Temperature dependence : Coulomb blockade vs coherent transport.

δR vs T obtained from SGM maps with V_tip = −1 V (circles) and from data in ref. (squares). The dashed line corresponds to a T⁻¹ dependence. The gray region corresponds to an exponential dependence exp(−T/T₀) with 9.5 K < T₀ < 19.1 K, consistent with magnetoresistance data and edge state velocity estimate along Ref. . The solid line corresponds to T₀ = 16.2 K, consistent with the spectroscopy data (see text).

Figure 4. Evidence for coherent transport in spectroscopy.

(a) dR/dV_tip as a function of the dc component of V_tip and V_bias at B = 9.5 T and T = 100 mK. Voltage modulation of V_tip was set to 50 mV. (b) 2D fit of dR/dV_tip using Eq. (2). (c–d) Transresistance vs V_bias taken along the red (c) and blue (d) dashed lines in (a–b). The circles correspond to the experimental data and the continuous lines to the fit.

Figure 5. Potential landscape and tunnelling paths across the QPC.

(a) Schematic representation of the electrostatic potential in the vicinity of the QPC (in brown), with the ES in yellow and the tunnelling paths connecting opposite ES (red and green). Only one edge state is represented, for the sake of clarity. (b) top view of the three-dimensional figure in (a), with the various tunnelling probabilities T_i between edge states.