A scale-space method for detecting recurrent DNA copy number changes with analytical false discovery rate control

Abstract

Tumor formation is partially driven by DNA copy number changes, which are typically measured using array comparative genomic hybridization, SNP arrays and DNA sequencing platforms. Many techniques are available for detecting recurring aberrations across multiple tumor samples, including CMAR, STAC, GISTIC and KC-SMART. GISTIC is widely used and detects both broad and focal (potentially overlapping) recurring events. However, GISTIC performs false discovery rate control on probes instead of events. Here we propose Analytical Multi-scale Identification of Recurrent Events, a multi-scale Gaussian smoothing approach, for the detection of both broad and focal (potentially overlapping) recurring copy number alterations. Importantly, false discovery rate control is performed analytically (no need for permutations) on events rather than probes. The method does not require segmentation or calling on the input dataset and therefore reduces the potential loss of information due to discretization. An important characteristic of the approach is that the error rate is controlled across all scales and that the algorithm outputs a single profile of significant events selected from the appropriate scales. We perform extensive simulations and showcase its utility on a glioblastoma SNP array dataset. Importantly, ADMIRE detects focal events that are missed by GISTIC, including two events involving known glioma tumor-suppressor genes: CDKN2C and NF1.

Figure 1.

Illustrating the steps involved for detecting recurring aberration in multiple copy number alteration profiles with the multi-scale ADMIRE approach. All plots in the left column, Column I, represent data with recurrent events, and Column II shows the exact same procedure when permuting the data to construct a cyclic shift null hypothesis. Column I: (A) Illustration of five (of 100) simulated aCGH profiles with recurring events and a number of passenger (random) aberrations. (B) The first step in detecting recurring events is to sum all profiles (100 samples) to a single aggregated profile. (C) A Gaussian kernel is convolved with the aggregated profile and z-normalized, as described in the text. This is done with many different kernel widths so that focal events can be detected with small kernels and broad events with larger kernels. Ultimately, constant thresholds (derived from the empirical null as outlined in Column II) will be applied on the smoothed signal (both upper and lower tail), as illustrated by the red dashed lines. (D) Illustration of how we combine all the events found on multiple scales. Basically, we take the union of all events found on all scales; however, for all kernels (except the smallest), we perform a filtering procedure to ensure the proper resolution. The procedure is simple in that we only keep those events that are substantially (20 times) larger then the kernel width (more on this in the text). Column II: Illustration of the permutation of profiles where each profile’s probes are cyclically shifted with a random offset (Panel A) and the summation of the resulting profiles (Panel B) to obtain a representative null hypothesis that closely resembles a stationary Gaussian random process with parameters and the auto-correlation r. Panel C shows the kernel convolution per scale. In this illustration, we propose to repeat the steps in Panels A, B and C one thousand times to obtain an empirical approximation of the null distribution and use these distributions to derive a threshold per scale corresponding to the desired control of FDR and FWER. However, in this article, we derive an analytical relationship between the thresholds and FWER or FDR.

Figure 2.

Illustration showing how power can be gained by considering multiple scales (levels of smoothing). (A) A simulated aggregated profile with two broad recurring gains and one focal gain embedded in a broad event. (B) Significance level of the aggregated profile for little smoothing (small kernel width). Owing to the small kernel width, the resolution is high and the boundaries on the detected regions are fairly accurate. This is at the expense of power and results in hundreds of significant segments instead of two broad events. (C) Significant power is gained for intermediate kernel widths and the two broad events are found as desired. Furthermore, the resolution is high enough (the segment size is much greater than the kernel width) and therefore the boundaries of the significant events are sufficiently accurate (compared with the aberration size). (D) High power is observed for large kernel widths (significance level exceeds the threshold by far) but the resolution is so low that two events are merged into one and boundary estimates are poor. (E) We obtain the final estimate of recurring segments by taking the union of all detected events on all scales that reveal sufficient resolution. Note that the focal events embedded in broad events are completely missed. Furthermore, significance in these figures is represented by the expected number of events found across the whole genome (as predicted by the null hypothesis). The threshold is selected at , a close upper-bound for the FWER of 0.01.

Figure 3.

Illustrating the recursive multi-level detection methodology. (A) On recursive level 1, we detect recurrent aberrations with the proposed multi-scale methodology. Note that the region in which we finally estimate the null parameters ( and r) is restricted to , as illustrated by the dotted line at the top of the figure. (B) On recursive level 2, we follow the exact same procedure, except this time, estimate the null parameters in the broad event . This allows us to detect embedded focal events inside broader events.

Figure 4.

Probe-based versus event-based FDR control. Illustration on how controlling the probe-based FDR (expected proportion of detected probes that are false-positives) can introduce an unexpected proportion of focal events simply due to the presence of broad chromosomal recurring aberrations.

Figure 5.

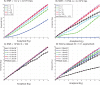
Illustration of the relationship between the analytical estimates of (x-axis) and that measured across 1000 simulations (y-axis) of aCGH profiles containing only passenger events. (A) We fix the kernel width to be small (40 kb) and the SNR at 1 to represent measurement noise. We vary the number of samples to aggregate for each simulation experiment. (B) A similar experiment on simulated aCGH profiles where we added no measurement noise () and therefore effectively work with segmented samples. The black line depicts the result obtained when using cyclic permutation to create a null hypothesis on the glioma dataset. (C) The number of simulated samples to aggregate is fixed at 100 and the kernel width is varied, showing good theoretical predictions for all kernels. The black line indicates the mean number of events detected when we apply multi-scale selection. (D) Similar results are depicted when using cyclic permutations to create a null hypothesis on the glioma dataset. The genome size for the simulated data is only bps, whereas the glioma dataset consists of all probes stretching from chromosome 1 to 22. Error bars indicate the standard error of the empirical .

Figure 6.

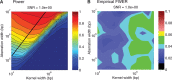
(A) A representative plot of the power for detecting a recurring aberration as a function of the aberration size and kernel width for the SNR fixed at 1. In this experiment, we added only a single recurring aberration per experiment and fixed at 5%. The black line indicates the maximum allowed kernel width at which an aberration can be detected if we apply filtering with in the multi-scale methodology. See Supplementary Figure S3 for similar plots at different SNRs. (B) The empirical FWER. The green regions indicate that the measured FWER is within 1 standard deviation of the expected 5% FWER.

Figure 7.

The relationship between the theoretically predicted analytical FDR and empirical FDR and power for a simulated dataset. (A) The empirical FDR (left panel) and power (right panel) as a function of the analytical FDR (varied between 1 and 25%) for the number of true focal recurrent events assuming the following values, , while keeping the number of samples to aggregate per simulation fixed at 200, i.e. . Furthermore, we do not add any noise, as the , implying that all samples are segmented. (B) The empirical FDR (left panel) and power (right panel) as a function of the number of samples to aggregate S for the SNR assuming the following values, , while keeping the number of focal recurrent events and FDR fixed at 50 () and 5%, respectively.

Figure 8.

Comparison of detected recurring events detected by ADMIRE and GISTIC2.0 on the glioma dataset. (A) Summary of the recurrent aberrations found by both ADMIRE and GISTIC2.0 on the entire genome. (A.I) The SNP array profiles for 141 glioma samples. Red (green) represents amplifications (deletions). (A.II) The sum of all the SNP array profiles. (A.III) A multi-level representation of the recurring events found by ADMIRE at 25% event-based FDR. The first recursive level shows all the broad and focal events that are not embedded in broad events. The second level shows more focal (or less broad) events embedded in broad first-level events, etc. (A.IV) Results found by GISTIC2.0 at 25% probe-based FDR. The first level (+1/−1 for gains or losses, respectively) represents all the broad recurrent events found at the chromosome arm level. After removing segments that stretch across whole chromosome arms, all segments with q-values below 0.25 are represented on the second level. Finally, focal regions are detected using the RegBounder algorithm and represented on the third level. Therefore, red events (positive levels) represent recurring gains (levels move upwards) and black (negative levels) represents deletions (with levels moving downwards). (B) A zoom of the result in Panel A, showing the first part of chromosome 1p. (C) The top recursive level (most focal) event found by ADMIRE containing the CHD5 gene. It is interesting to note that GISTIC2.0 finds a much more focal area close to CHD5; however, with careful observation of the aggregated profile in (B.II) it is obvious that no focal event can be called with high significance by ADMIRE at this point. (D) Shows the recurring region found by ADMIRE containing the known glioma tumor suppressor gene CDKN2C that was missed by GISTIC2.0.