From mechanical folding trajectories to intrinsic energy landscapes of biopolymers
- PMID: 23487746
- PMCID: PMC3606983
- DOI: 10.1073/pnas.1214051110
From mechanical folding trajectories to intrinsic energy landscapes of biopolymers
Abstract
In single-molecule laser optical tweezer (LOT) pulling experiments, a protein or RNA is juxtaposed between DNA handles that are attached to beads in optical traps. The LOT generates folding trajectories under force in terms of time-dependent changes in the distance between the beads. How to construct the full intrinsic folding landscape (without the handles and beads) from the measured time series is a major unsolved problem. By using rigorous theoretical methods--which account for fluctuations of the DNA handles, rotation of the optical beads, variations in applied tension due to finite trap stiffness, as well as environmental noise and limited bandwidth of the apparatus--we provide a tractable method to derive intrinsic free-energy profiles. We validate the method by showing that the exactly calculable intrinsic free-energy profile for a generalized Rouse model, which mimics the two-state behavior in nucleic acid hairpins, can be accurately extracted from simulated time series in a LOT setup regardless of the stiffness of the handles. We next apply the approach to trajectories from coarse-grained LOT molecular simulations of a coiled-coil protein based on the GCN4 leucine zipper and obtain a free-energy landscape that is in quantitative agreement with simulations performed without the beads and handles. Finally, we extract the intrinsic free-energy landscape from experimental LOT measurements for the leucine zipper.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

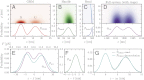
 for each component type in the system: (A) GRM, (B) dsDNA handle, (C) polystyrene bead. Handle, bead, and trap parameters are listed in
for each component type in the system: (A) GRM, (B) dsDNA handle, (C) polystyrene bead. Handle, bead, and trap parameters are listed in  . (Lower) Projection onto z alone. (D) Result for the total system end-to-end distribution
. (Lower) Projection onto z alone. (D) Result for the total system end-to-end distribution  tot derived by convolving the component probabilities and accounting for the optical traps. (E–G) Construction of the original GRM distribution
tot derived by convolving the component probabilities and accounting for the optical traps. (E–G) Construction of the original GRM distribution  starting from
starting from  tot. (E)
tot. (E)  tot (purple) and
tot (purple) and  (blue) as a function of z on the bottom axis, measured relative to
(blue) as a function of z on the bottom axis, measured relative to  , the average extension for each distribution. For
, the average extension for each distribution. For  tot, the upper axis shows the z range translated into the corresponding trap forces F. After removing the trap effects,
tot, the upper axis shows the z range translated into the corresponding trap forces F. After removing the trap effects,  is the distribution for constant force F0 = 11.9 pN. (F)
is the distribution for constant force F0 = 11.9 pN. (F)  , describing the total probability at F0 of fluctuations resulting from both handles and the rotation of the beads. (G) Constructed solution for
, describing the total probability at F0 of fluctuations resulting from both handles and the rotation of the beads. (G) Constructed solution for  (solid line), obtained by numerically inverting the convolution
(solid line), obtained by numerically inverting the convolution  . Exact analytical result for
. Exact analytical result for  is shown as a dashed line; zN is the position of the N peak.
is shown as a dashed line; zN is the position of the N peak.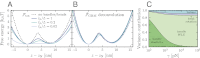
 tot for fixed L = 100 nm, and varying ratios lp/L. All of the other parameters are in
tot for fixed L = 100 nm, and varying ratios lp/L. All of the other parameters are in  , is shown for comparison. (B) For each ℱtot in A, the construction of
, is shown for comparison. (B) For each ℱtot in A, the construction of  at F0, together with the exact answer (dashed line). (C) For system parameters matching the experiment (
at F0, together with the exact answer (dashed line). (C) For system parameters matching the experiment ( broken down into the individual handle, bead, and linker contributions. The fraction for each component is shown as a function of varying handle elastic modulus γ.
broken down into the individual handle, bead, and linker contributions. The fraction for each component is shown as a function of varying handle elastic modulus γ.
 at F0 = 12.3 pN vs. end-to-end extension z. (Right) Representative protein configurations from the four wells (N, I1, I2, U), with asparagine residues colored blue. (B) Average fraction of native contacts between the two alpha-helical strands of LZ26 (the “zipper bonds”) as a function of z. (Left) Lists of the a and d residues in the heptads making up the amino acid sequence for each LZ26 strand, placed according to their position along the zipper. Asparagines (N) are highlighted in blue. (C) For the residues listed in B, the residue contact energies used in the SOP simulation [rescaled BT (30) values].
at F0 = 12.3 pN vs. end-to-end extension z. (Right) Representative protein configurations from the four wells (N, I1, I2, U), with asparagine residues colored blue. (B) Average fraction of native contacts between the two alpha-helical strands of LZ26 (the “zipper bonds”) as a function of z. (Left) Lists of the a and d residues in the heptads making up the amino acid sequence for each LZ26 strand, placed according to their position along the zipper. Asparagines (N) are highlighted in blue. (C) For the residues listed in B, the residue contact energies used in the SOP simulation [rescaled BT (30) values].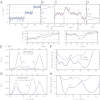
 from SOP simulations of the LZ26 leucine zipper at constant force F0 = 12.3 pN in the absence of handles/beads. (C and D) A trajectory fragment and the total system distribution
from SOP simulations of the LZ26 leucine zipper at constant force F0 = 12.3 pN in the absence of handles/beads. (C and D) A trajectory fragment and the total system distribution  tot at ztrap = 503 nm. C shows both the total extension ztot(t) (purple) and the protein extension zp(t) (gray). Triangles mark times when the protein makes a transition between states, and the arrows point to two enlarged portions of the trajectories. In all cases the z-axis origin is zI1, the peak location of the I1 intermediate state. (E–G) Leucine zipper free-energy profiles extracted from time series (third row = simulation, fourth row = experiment). First column shows the total system end-to-end distribution
tot at ztrap = 503 nm. C shows both the total extension ztot(t) (purple) and the protein extension zp(t) (gray). Triangles mark times when the protein makes a transition between states, and the arrows point to two enlarged portions of the trajectories. In all cases the z-axis origin is zI1, the peak location of the I1 intermediate state. (E–G) Leucine zipper free-energy profiles extracted from time series (third row = simulation, fourth row = experiment). First column shows the total system end-to-end distribution  tot and the corresponding
tot and the corresponding  at constant force F0 = 12.3 pN. In the experimental case F0 = 12.3 ± 0.9 pN is the midpoint force at which the I1 and U states are equally likely. For
at constant force F0 = 12.3 pN. In the experimental case F0 = 12.3 ± 0.9 pN is the midpoint force at which the I1 and U states are equally likely. For  tot, ztrap = 503 nm (simulation), 1553 ± 1 nm (experiment). Force scales at the top are the range of trap forces for
tot, ztrap = 503 nm (simulation), 1553 ± 1 nm (experiment). Force scales at the top are the range of trap forces for  tot. Second column shows the computed intrinsic protein free-energy profiles
tot. Second column shows the computed intrinsic protein free-energy profiles  compared with the total system profile, ℱtot (shifted upward for clarity). (F) SOP simulations for the protein alone at constant F0 provide a reference landscape, drawn as a dashed line. (H) Dotted curve is the reconstructed
compared with the total system profile, ℱtot (shifted upward for clarity). (F) SOP simulations for the protein alone at constant F0 provide a reference landscape, drawn as a dashed line. (H) Dotted curve is the reconstructed  at the midpoint force F0 = 12.1 ± 0.9 pN, from a second, independent experimental trajectory, with ztrap = 1547 ± 1 nm.
at the midpoint force F0 = 12.1 ± 0.9 pN, from a second, independent experimental trajectory, with ztrap = 1547 ± 1 nm.  curves have a median uncertainty of 0.4 kBT over the plotted range (see
curves have a median uncertainty of 0.4 kBT over the plotted range (see References
-
- Thirumalai D, Hyeon C. RNA and protein folding: Common themes and variations. Biochemistry. 2005;44(13):4957–4970. - PubMed
-
- Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. - PubMed
-
- Thirumalai D, O’Brien EP, Morrison G, Hyeon C. Theoretical perspectives on protein folding. Annu Rev Biophys. 2010;39:159–183. - PubMed
-
- Guo Z, Thirumalai D. Kinetics of protein folding: Nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36(1):83–102.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

