Improving basic and translational science by accounting for litter-to-litter variation in animal models
- PMID: 23522086
- PMCID: PMC3661356
- DOI: 10.1186/1471-2202-14-37
Improving basic and translational science by accounting for litter-to-litter variation in animal models
Abstract
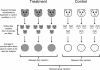
Background: Animals from the same litter are often more alike compared with animals from different litters. This litter-to-litter variation, or "litter effects", can influence the results in addition to the experimental factors of interest. Furthermore, sometimes an experimental treatment can only be applied to whole litters rather than to individual offspring. An example is the valproic acid (VPA) model of autism, where VPA is administered to pregnant females thereby inducing the disease phenotype in the offspring. With this type of experiment the sample size is the number of litters and not the total number of offspring. If such experiments are not appropriately designed and analysed, the results can be severely biased as well as extremely underpowered.
Results: A review of the VPA literature showed that only 9% (3/34) of studies correctly determined that the experimental unit (n) was the litter and therefore made valid statistical inferences. In addition, litter effects accounted for up to 61% (p<0.001) of the variation in behavioural outcomes, which was larger than the treatment effects. In addition, few studies reported using randomisation (12%) or blinding (18%), and none indicated that a sample size calculation or power analysis had been conducted.
Conclusions: Litter effects are common, large, and ignoring them can make replication of findings difficult and can contribute to the low rate of translating preclinical in vivo studies into successful therapies. Only a minority of studies reported using rigorous experimental methods, which is consistent with much of the preclinical in vivo literature.
Figures

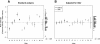

References
-
- Geerts H. Of mice and men: bridging the translational disconnect in CNS drug discovery. CNS Drugs. 2009;23(11):915–926. doi: 10.2165/11310890-000000000-00000. [ http://dx.doi.org/10.2165/11310890-000000000-00000] - DOI - DOI - PubMed
-
- Hughes CW. Outcome of early experience studies as affected by between-litter variance. J Nutr. 1979;109(4):642–645. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

