Modeling and simulation of biological systems from image data
- PMID: 23533152
- PMCID: PMC3674526
- DOI: 10.1002/bies.201200051
Modeling and simulation of biological systems from image data
Abstract
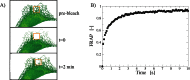
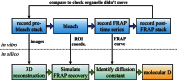
This essay provides an introduction to the terminology, concepts, methods, and challenges of image-based modeling in biology. Image-based modeling and simulation aims at using systematic, quantitative image data to build predictive models of biological systems that can be simulated with a computer. This allows one to disentangle molecular mechanisms from effects of shape and geometry. Questions like "what is the functional role of shape" or "how are biological shapes generated and regulated" can be addressed in the framework of image-based systems biology. The combination of image quantification, model building, and computer simulation is illustrated here using the example of diffusion in the endoplasmic reticulum.
Copyright © 2013 WILEY Periodicals, Inc.
Figures



Similar articles
-
Effects of organelle shape on fluorescence recovery after photobleaching.Biophys J. 2005 Sep;89(3):1482-92. doi: 10.1529/biophysj.104.057885. Epub 2005 Jun 10. Biophys J. 2005. PMID: 15951382 Free PMC article.
-
Simulations of (an)isotropic diffusion on curved biological surfaces.Biophys J. 2006 Feb 1;90(3):878-85. doi: 10.1529/biophysj.105.073809. Epub 2005 Nov 11. Biophys J. 2006. PMID: 16284262 Free PMC article.
-
Analysis of protein and lipid dynamics using confocal fluorescence recovery after photobleaching (FRAP).Curr Protoc Cytom. 2012 Oct;Chapter 2:Unit2.19. doi: 10.1002/0471142956.cy0219s62. Curr Protoc Cytom. 2012. PMID: 23042527 Free PMC article.
-
Toward the virtual cell: automated approaches to building models of subcellular organization "learned" from microscopy images.Bioessays. 2012 Sep;34(9):791-9. doi: 10.1002/bies.201200032. Epub 2012 Jul 10. Bioessays. 2012. PMID: 22777818 Free PMC article. Review.
-
Image-based systems biology of infection.Cytometry A. 2015 Jun;87(6):462-70. doi: 10.1002/cyto.a.22638. Epub 2015 Jan 29. Cytometry A. 2015. PMID: 25641512 Review.
Cited by
-
Tracing the footsteps of autophagy in computational biology.Brief Bioinform. 2021 Jul 20;22(4):bbaa286. doi: 10.1093/bib/bbaa286. Brief Bioinform. 2021. PMID: 33201177 Free PMC article.
-
VascuViz: a multimodality and multiscale imaging and visualization pipeline for vascular systems biology.Nat Methods. 2022 Feb;19(2):242-254. doi: 10.1038/s41592-021-01363-5. Epub 2022 Feb 10. Nat Methods. 2022. PMID: 35145319 Free PMC article.
-
Stability selection enables robust learning of differential equations from limited noisy data.Proc Math Phys Eng Sci. 2022 Jun;478(2262):20210916. doi: 10.1098/rspa.2021.0916. Epub 2022 Jun 15. Proc Math Phys Eng Sci. 2022. PMID: 35756878 Free PMC article.
-
A versatile pipeline for the multi-scale digital reconstruction and quantitative analysis of 3D tissue architecture.Elife. 2015 Dec 27;4:e11214. doi: 10.7554/eLife.11214. Elife. 2015. PMID: 26673893 Free PMC article.
-
Dancing with the Stars: Using Image Analysis to Study the Choreography of the Endoplasmic Reticulum and Its Partners and of Movement Within Its Tubules.Methods Mol Biol. 2024;2772:87-114. doi: 10.1007/978-1-0716-3710-4_7. Methods Mol Biol. 2024. PMID: 38411808
References
-
- Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–4. - PubMed
-
- Kitano H. Computational systems biology. Nature. 2002;420:206–10. - PubMed
-
- Wolkenhauer O. Systems biology: the reincarnation of systems theory applied in biology. Brief Bioinform. 2001;2:258. - PubMed
-
- Collinet C, Stöter M, Bradshaw CR, Samusik N, et al. Systems survey of endocytosis by multiparametric image analysis. Nature. 2010;464:243–9. - PubMed
-
- Kohl P, Noble D, Winslow R, Hunter PJ. Computational modeling of biological systems: tools and visions. Phil Trans R Soc Lond A. 2000;358:579–610.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

