Morphogen transport
- PMID: 23533171
- PMCID: PMC3621481
- DOI: 10.1242/dev.083519
Morphogen transport
Abstract
The graded distribution of morphogens underlies many of the tissue patterns that form during development. How morphogens disperse from a localized source and how gradients in the target tissue form has been under debate for decades. Recent imaging studies and biophysical measurements have provided evidence for various morphogen transport models ranging from passive mechanisms, such as free or hindered extracellular diffusion, to cell-based dispersal by transcytosis or cytonemes. Here, we analyze these transport models using the morphogens Nodal, fibroblast growth factor and Decapentaplegic as case studies. We propose that most of the available data support the idea that morphogen gradients form by diffusion that is hindered by tortuosity and binding to extracellular molecules.
Figures


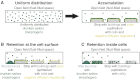
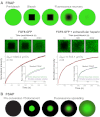
 ; purple), which leads to the concentration of morphogen in the tissue layer and to exclusion from the fluid-filled space. In an extended model,
; purple), which leads to the concentration of morphogen in the tissue layer and to exclusion from the fluid-filled space. In an extended model,  is converted into an irreversibly trapped fraction,
is converted into an irreversibly trapped fraction,  , with a clearance rate constant kt.
, with a clearance rate constant kt.
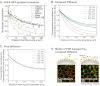
 is degraded with a degradation rate constant k1. In both the free and hindered diffusion models, the free extracellular concentration of morphogens is low. (C) The free and hindered diffusion models can lead to the same steady state morphogen distribution but predict distinct gradient formation kinetics. The free diffusion model predicts rapid progression to the final shape of the distribution, whereas hindered diffusion models predict slow progression. Shown are the curves from the first graphs in A and B normalized to the respective concentrations at the source boundary. Simulations were performed similar to those of Müller et al. (Müller et al., 2012) using a two-dimensional geometry of 200 μm length and 12 μm height; source width of 10 μm; fluid-filled space height of 6 μm; no-flux boundary conditions; initial morphogen concentrations of zero; concentration gradients were sampled in the middle of the target field at a height of 3 μm. Parameters used: (A) simple model, D=20 μm2/s, k1=0.1/s; extended model, D=20 μm2/s, kt=0.1/s, k1=0.000076/s; (B) simple model, D=20 μm2/s, kon=0.001/(nM·s), koff=0.021/s, k1=0.00024/s, initial concentration of R in source and target field Rinit=10 μM [kon, koff and Rinit were chosen based on values in the literature (Dowd et al., 1999; Umulis et al., 2009)]; extended model, D=20 μm2/s, kon=0.001/(nM·s), koff=0.021/s, kt=0.00024/s, k1=0.000076/s, Rinit=10 μM. In all models, production of the mobile morphogen only occurred in the source at a constant rate of v=0.2 pM/s. The source and target field were modeled without the effects of cells and tortuosity. Tortuosity could reduce the values of D that were used in the models, and the clearance rate and off-rate constants would change accordingly.
is degraded with a degradation rate constant k1. In both the free and hindered diffusion models, the free extracellular concentration of morphogens is low. (C) The free and hindered diffusion models can lead to the same steady state morphogen distribution but predict distinct gradient formation kinetics. The free diffusion model predicts rapid progression to the final shape of the distribution, whereas hindered diffusion models predict slow progression. Shown are the curves from the first graphs in A and B normalized to the respective concentrations at the source boundary. Simulations were performed similar to those of Müller et al. (Müller et al., 2012) using a two-dimensional geometry of 200 μm length and 12 μm height; source width of 10 μm; fluid-filled space height of 6 μm; no-flux boundary conditions; initial morphogen concentrations of zero; concentration gradients were sampled in the middle of the target field at a height of 3 μm. Parameters used: (A) simple model, D=20 μm2/s, k1=0.1/s; extended model, D=20 μm2/s, kt=0.1/s, k1=0.000076/s; (B) simple model, D=20 μm2/s, kon=0.001/(nM·s), koff=0.021/s, k1=0.00024/s, initial concentration of R in source and target field Rinit=10 μM [kon, koff and Rinit were chosen based on values in the literature (Dowd et al., 1999; Umulis et al., 2009)]; extended model, D=20 μm2/s, kon=0.001/(nM·s), koff=0.021/s, kt=0.00024/s, k1=0.000076/s, Rinit=10 μM. In all models, production of the mobile morphogen only occurred in the source at a constant rate of v=0.2 pM/s. The source and target field were modeled without the effects of cells and tortuosity. Tortuosity could reduce the values of D that were used in the models, and the clearance rate and off-rate constants would change accordingly.




References
-
- Ayers K. L., Gallet A., Staccini-Lavenant L., Thérond P. P. (2010). The long-range activity of Hedgehog is regulated in the apical extracellular space by the glypican Dally and the hydrolase Notum. Dev. Cell 18, 605–620 - PubMed
-
- Baeg G. H., Selva E. M., Goodman R. M., Dasgupta R., Perrimon N. (2004). The Wingless morphogen gradient is established by the cooperative action of Frizzled and Heparan Sulfate Proteoglycan receptors. Dev. Biol. 276, 89–100 - PubMed
-
- Beck S., Le Good J. A., Guzman M., Ben Haim N., Roy K., Beermann F., Constam D. B. (2002). Extraembryonic proteases regulate Nodal signalling during gastrulation. Nat. Cell Biol. 4, 981–985 - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

