Angiogenesis: an adaptive dynamic biological patterning problem

Abstract

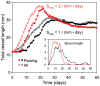
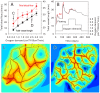
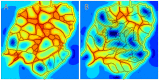
Formation of functionally adequate vascular networks by angiogenesis presents a problem in biological patterning. Generated without predetermined spatial patterns, networks must develop hierarchical tree-like structures for efficient convective transport over large distances, combined with dense space-filling meshes for short diffusion distances to every point in the tissue. Moreover, networks must be capable of restructuring in response to changing functional demands without interruption of blood flow. Here, theoretical simulations based on experimental data are used to demonstrate that this patterning problem can be solved through over-abundant stochastic generation of vessels in response to a growth factor generated in hypoxic tissue regions, in parallel with refinement by structural adaptation and pruning. Essential biological mechanisms for generation of adequate and efficient vascular patterns are identified and impairments in vascular properties resulting from defects in these mechanisms are predicted. The results provide a framework for understanding vascular network formation in normal or pathological conditions and for predicting effects of therapies targeting angiogenesis.

Figure 1. Concepts of microvascular pattern formation.

(A) Microvascular networks are often conceptualized as mesh or hierarchical structures. A mesh minimizes diffusion distances between capillaries and tissue but has high flow resistance and results in non-uniform oxygen levels from the arterial to the venous side. In a hierarchical structure, larger supply vessels decrease flow resistance, but regions surrounding those vessels are inadequately supplied due to large diffusion distances. Colors (red - green - blue) indicate flow from arterial to venous vessels, with decline in oxygen levels. (B) Hypothesized steps in generation of functional vascular networks. A dense network of vessels is generated by over-abundant angiogenesis and refined by structural adaptation and pruning. Resulting networks combine features of mesh and hierarchical structures.

Figure 2. Steps in simulation approach.

(A) Network of microvessels in rat mesentery, imaged using intravital microscopy. Shaded overlay highlights vessel positions, with arterioles (red), capillaries (green) and venules (blue). This region was selected for analysis because the outer loop of venules provides stable boundary conditions for the tissue domain. (B) Computer generated image of network structure, trimmed to reduce the number of network boundary nodes to five (arrows). (C) Network skeleton, used as initial condition for simulations. In (D–I), a small region within a typical simulation is shown at a sequence of times indicating aspects of the method. White triangles denote features mentioned in this caption. (D) The oxygen field surrounding the vessels is computed using the Green's function method. Blue shades denote low oxygen levels. VEGF is assumed to be generated in hypoxic regions and to diffuse according to local gradients, and the resulting VEGF field is computed. Diagonal hatching indicates VEGF concentration above a given threshold. (E) On vessels lying in regions with VEGF above threshold, sprouts are generated with probability dependent on local VEGF concentration. (F) A fixed rate of sprout elongation is assumed. Direction of growth is randomly varied at each time step. (G) If other vessels lie within a sector of radius 100 µm ahead of the sprout tip, the growth is biased towards them. (H) A sprout reaching another vessel forms a connection, allowing flow. (I) Diameters of flowing vessels adapt to metabolic and hemodynamic stimuli.

Figure 3. Bifurcation angles resulting from vessel sprouting and connection.

(A) A sprout at 90° to the parent vessel creates initial bifurcation angles of 90°, 90° and 180°. A sprout forming a connection to an existing vessel creates initial bifurcation angles of θ, 180°−θ and 180°, where θ depends on the direction from which the sprout approaches. (B) Migration through the tissue (short blue arrows) driven by tension in each segment and the resulting imbalance of forces acting within the network results in a reduction of the 180° bifurcation angle and increases in the other two angles.

Figure 4. Simulated angiogenesis, showing oxygen and VEGF distributions.

Oxygen levels in vessels and tissue are color coded according to scale at right. Dark blue indicates hypoxic tissue. Diagonal shading indicates VEGF above threshold concentration. Time (t) in days and total vessel length (L) in mm are indicated. Maximal rate of sprout formation is 2 mm⁻¹day⁻¹. Tissue oxygen demand is 2 cm³/100 cm³/min. (A) Initial configuration. (B) Sprouts (white arrows) and a short flow pathway between arterioles and venules (a-v shunt, purple arrow) are generated. (C) More complex flow pathways form, leading to improved oxygenation (lower right region). (D) Improved oxygenation leads to decreased VEGF levels. Structural adaptation causes pruning of the a-v shunt (purple arrow), but some redundant flow pathways remain (black arrows). Total vessel length reaches its maximum. (E) Structural adaptation leads to pruning of redundant flow pathways (black arrows). (F) Final refined network. Virtually no hypoxia remains and VEGF levels are generally below threshold. See online supplement, Video S1, for movie clip.

Figure 5. Comparison of simulated and observed network characteristics.

Simulated oxygen and VEGF distributions in experimentally observed network (A), and in simulated angiogenesis at t = 200 days (B). The observed network structure is derived from the image shown in Figure 2A. The network at t = 200 days was derived from the same initial network as shown in Figure 4A but with a different seed for random number generation. Oxygen demand, rate of sprout formation, length scale, color coding of oxygen levels and diagonal shading indicating VEGF above threshold are as in Figure 4. (C) Frequency distribution of distance of tissue points to nearest vessel. (D) Frequency distribution of oxygen levels at tissue points. Results for simulated networks are mean ± standard deviation for n = 6 simulations with different seeds for random number generation.

Figure 6. Effect of tension-induced vessel migration on distribution of branching angles.

(A) Example of network structure generated when tension-induced migration is suppressed, at t = 200 days. Other conditions are as in Figure 4. (B) Distribution of branching angles for network shown in A. (C) Distribution of branching angles for observed network structure. (D) Distribution of branching angles for network shown in Figure 4 at t = 200 days, including tension-induced migration.

Figure 7. Dynamics of network generation.

Variation of total vessel length during an individual simulation of angiogenesis. Main plot: vessel length. Inset: length of non-flowing sprouts. Initially, total length increases rapidly due to sprouting. After sprouts form connections, flowing length increases. When sprout formation rate is 2 mm⁻¹day⁻¹ (red curves), summed vessel length shows a strong peak at 20 days and then decreases, stabilizing after 50 days. For reduced sprout formation rate (1 mm⁻¹day⁻¹, black curves), peak vascular length is reduced, stabilization takes longer and total vessel length remains higher.

Figure 8. Variation of network properties with oxygen demand.

(A) Total blood flow and vessel length at t = 200 days, for fixed arteriole-venule pressure drop (mean ± s.d. for 6–12 runs). (B) Time-dependent response of total vessel length to step changes in demand. Lower curve: oxygen demand. Upper curves: total vessel length (flowing, all, mean of 3 runs). (C, D) Network structures for demand 0.5 and 2.5 cm³/100 cm³/min. Length and color scales as in Figure 4.

Figure 9. Effects of inhibiting adaptation or conducted responses.

(A) Angiogenesis without structural adaptation and pruning. Resulting structure is mesh-like, without hierarchical structure. (B) Simulation of angiogenesis with reduced conducted response strength. Short flow pathways from feeding to draining vessels carry most of the flow. Regions remote from feeding vessels receive inadequate perfusion. Length and color scales as in Figure 4.