Models in animal collective decision-making: information uncertainty and conflicting preferences
- PMID: 23565335
- PMCID: PMC3293206
- DOI: 10.1098/rsfs.2011.0090
Models in animal collective decision-making: information uncertainty and conflicting preferences
Abstract
Collective decision-making plays a central part in the lives of many social animals. Two important factors that influence collective decision-making are information uncertainty and conflicting preferences. Here, I bring together, and briefly review, basic models relating to animal collective decision-making in situations with information uncertainty and in situations with conflicting preferences between group members. The intention is to give an overview about the different types of modelling approaches that have been employed and the questions that they address and raise. Despite the use of a wide range of different modelling techniques, results show a coherent picture, as follows. Relatively simple cognitive mechanisms can lead to effective information pooling. Groups often face a trade-off between decision accuracy and speed, but appropriate fine-tuning of behavioural parameters could achieve high accuracy while maintaining reasonable speed. The right balance of interdependence and independence between animals is crucial for maintaining group cohesion and achieving high decision accuracy. In conflict situations, a high degree of decision-sharing between individuals is predicted, as well as transient leadership and leadership according to needs and physiological status. Animals often face crucial trade-offs between maintaining group cohesion and influencing the decision outcome in their own favour. Despite the great progress that has been made, there remains one big gap in our knowledge: how do animals make collective decisions in situations when information uncertainty and conflict of interest operate simultaneously?
Keywords: collective decisions; game-theory models; self-organizing systems.
Figures

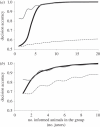
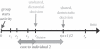
 and in a shared decision:
and in a shared decision:  whereby f(Δt) are the fitness costs to an individual of changing activity at a time that is different by Δt from its own optimal time.
whereby f(Δt) are the fitness costs to an individual of changing activity at a time that is different by Δt from its own optimal time.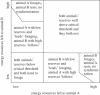

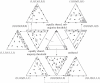

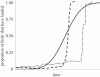
References
-
- Seeley T. D., Buhrman S. C. 1999. Group decision making in swarms of honey bees. Behav. Ecol. Sociobiol. 45, 19–3110.1007/s002650050536 (doi:10.1007/s002650050536) - DOI - DOI
-
- Conradt L., Roper T. J. 2005. Consensus decision making in animals. Trends Ecol. Evol. 20, 449–45610.1016/j.tree.2005.05.008 (doi:10.1016/j.tree.2005.05.008) - DOI - DOI - PubMed
-
- Trillmich J., Fichtel C., Kappeler P. M. 2004. Coordination of group movements in wild Verreaux's sifakas Propithecus verreauxi. Behaviour 141, 1103–112010.1163/1568539042664579 (doi:10.1163/1568539042664579) - DOI - DOI
-
- List C., Elsholtz C., Seeley T. D. 2009. Independence and interdependence in collective decision making: an agent-based model of nest-site choice by honeybee swarms. Phil. Trans. R. Soc. B 364, 755–76210.1098/rstb.2008.0277 (doi:10.1098/rstb.2008.0277) - DOI - DOI - PMC - PubMed
-
- Franks N. R., Dechaume-Moncharmont F. X., Hanmore E., Reynolds J. K. 2009. Speed versus accuracy in decision-making ants: expediting politics and policy implementation. Phil. Trans. R. Soc. B 364, 845–85210.1098/rstb.2008.0224 (doi:10.1098/rstb.2008.0224) - DOI - DOI - PMC - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous
