Mechanical forces in cerebral cortical folding: a review of measurements and models
- PMID: 23566768
- PMCID: PMC3842388
- DOI: 10.1016/j.jmbbm.2013.02.018
Mechanical forces in cerebral cortical folding: a review of measurements and models
Abstract
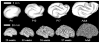
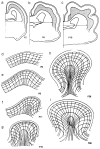
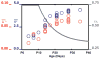
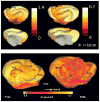
Folding of the cerebral cortical surface is a critical process in human brain development, yet despite decades of indirect study and speculation the mechanics of the process remain incompletely understood. Leading hypotheses have focused on the roles of circumferential expansion of the cortex, radial growth, and internal tension in neuronal fibers (axons). In this article, we review advances in the mathematical modeling of growth and morphogenesis and new experimental data, which together promise to clarify the mechanical basis of cortical folding. Recent experimental studies have illuminated not only the fundamental cellular and molecular processes underlying cortical development, but also the stress state and mechanical behavior of the developing brain. The combination of mathematical modeling and biomechanical data provides a means to evaluate hypothesized mechanisms objectively and quantitatively, and to ensure that they are consistent with physical law, given plausible assumptions and reasonable parameter values.
Copyright © 2013 Elsevier Ltd. All rights reserved.
Figures



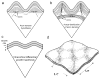
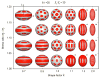

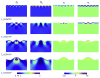
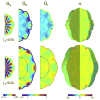
References
-
- Barron DH. An experimental analysis of some factors involved in the development of the fissure pattern of the cerebral cortex. Journal of Experimental Zoology. 1950;113:553–581.
-
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of Magnetic Resonance, Series B. 1996;111:209–219. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

