Independence is elusive: set size effects on encoding precision in visual search

Abstract

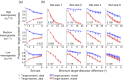
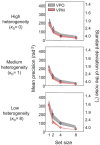
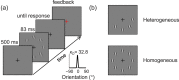
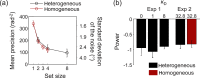
Looking for a target in a visual scene becomes more difficult as the number of stimuli increases. In a signal detection theory view, this is due to the cumulative effect of noise in the encoding of the distractors, and potentially on top of that, to an increase of the noise (i.e., a decrease of precision) per stimulus with set size, reflecting divided attention. It has long been argued that human visual search behavior can be accounted for by the first factor alone. While such an account seems to be adequate for search tasks in which all distractors have the same, known feature value (i.e., are maximally predictable), we recently found a clear effect of set size on encoding precision when distractors are drawn from a uniform distribution (i.e., when they are maximally unpredictable). Here we interpolate between these two extreme cases to examine which of both conclusions holds more generally as distractor statistics are varied. In one experiment, we vary the level of distractor heterogeneity; in another we dissociate distractor homogeneity from predictability. In all conditions in both experiments, we found a strong decrease of precision with increasing set size, suggesting that precision being independent of set size is the exception rather than the rule.

Figure 1

How does precision depend on set size? Each box in the diagram represents a distractor condition in single-target visual search. The gray boxes represent conditions for which set size effects on precision have been studied previously: homogeneous distractors that are predictable on every trial (bottom left) and maximally heterogeneous distractors that are also maximally unpredictable (top right). In this paper, we interpolate between these conditions (Experiment 1) and dissociate the factors (Experiment 2).

Figure 2

Experiment 1. (a) Time course of a single trial. (b) Von Mises distributions from which the distractor orientations were drawn in the three conditions (low, medium, and high heterogeneity). (c) Sample search displays in the three conditions. Displays are not to scale.

Figure 3

Data from Experiment 1. Here and elsewhere, error bars indicate 1 SEM. (a) Mean performance for the three heterogeneity conditions. Each condition was presented in two out of six sessions. (b) Hit and false-alarm rates as a function of set size for each condition.

Figure 4

VPO model fits in Experiment 1. (a) Hit and false-alarm rates in the three heterogeneity conditions. Here and elsewhere, shaded areas indicate 1 SEM in the model, and numbers indicate the root-mean-square error between model and data, averaged over subjects. (b) Proportion “target present” responses as a function of the minimum target-distractor difference, separately for target-present (blue) and target-absent (red) trials. For set size 1, there are no distractors on target-present trials. Note that the values on the x-axes differ between rows.

Figure 5

Model comparison results for Experiment 1. Shown are BIC values of the EPO, EPM, and VPM models relative to the VPO model, for each subject (left) as well as the group averages (right). Each row corresponds to a heterogeneity condition. Higher BIC values mean worse fits.

Figure 6

Dependence of precision on set size in Experiment 1. Estimates of mean precision parameter at each set size in the VPO (black) and VPM (red) models. The right y-axis shows the corresponding standard deviation of the Gaussian noise distributions, computed using the mapping σ² = 1/(4J̄) (see Models). The shades represent the best-fitting power law (mean over subjects; width indicates 1 SEM).

Figure 7

Experiment 2. (a) Time course of a trial (heterogeneous condition). Distractor orientations were drawn from a Von Mises distribution with a concentration parameter κ_D = 32.8 (corresponding to 5°; inset). Subjects judged whether a vertical target was present among the stimuli. (b) In the heterogeneous condition, distractor orientations were drawn independently. In the homogeneous condition, a common distractor orientation was drawn on each trial and assigned to all distractors on that trial.

Figure 8

Data and VPO model fits from Experiment 2. Top row: homogeneous; bottom row: heterogeneous. (a) Hit and false alarm: data (circles and error bars) and VPO model fits (shaded areas). (b) Proportion “target present” responses as a function of the target-distractor difference, separately for target-present (blue) and target-absent (red) trials. For set size 1, there are no distractors on target-present trials. Note that the values on the x-axes and the set sizes are different in the homogeneous and heterogeneous conditions.

Figure 9

Comparison between conditions of the relationship between mean precision and set size in the VPO model. (a) Mean precision estimates for the heterogeneous (black) and homogeneous (red) conditions of Experiment 2. (b) Estimates of the power in the relationship between mean precision and set size for all conditions in Experiments 1 and 2.

Figure A1

Generative models. These diagrams depict the dependencies between the variable of interest (target presence, C) and the measurements (x). Part of the statistical structure is shared (top), and part of it is specific to the experiment (bottom). 0 is the zero vector, and 1_i is a vector of zeroes with a 1 in the i^th entry. VM stands for the Von Mises distribution on (−90°, 90°); in parentheses are its argument, its mean, and its concentration parameter.