Angular spectrum simulation of X-ray focusing by Fresnel zone plates
- PMID: 23592617
- PMCID: PMC3943547
- DOI: 10.1107/S090904951300263X
Angular spectrum simulation of X-ray focusing by Fresnel zone plates
Abstract
A computing simulation routine to model any type of circularly symmetric diffractive X-ray element has been implemented. The wavefield transmitted beyond the diffractive structures is numerically computed by the angular spectrum propagation method to an arbitrary propagation distance. Cylindrical symmetry is exploited to reduce the computation and memory requirements while preserving the accuracy of the numerical calculation through a quasi-discrete Hankel transform algorithm, an approach described by Guizar-Sicairos & Gutierrez-Vega [J. Opt. Soc. Am. A, (2004), 21, 53-58]. In particular, the code has been used to investigate the requirements for the stacking of two high-resolution Fresnel zone plates with an outermost zone width of 20 nm.
Keywords: Fresnel zone plate stacking; X-ray wavefield modeling; angular spectrum method; diffractive X-ray optics.
Figures
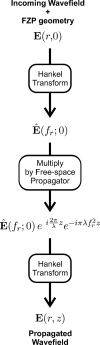
 . The angular spectrum of the initial wavefield,
. The angular spectrum of the initial wavefield,  , is calculated by a Hankel transform. Then, the propagated wavefield at a distance z,
, is calculated by a Hankel transform. Then, the propagated wavefield at a distance z,  , is obtained by multiplying
, is obtained by multiplying  by the free-space propagator
by the free-space propagator  and applying a second Hankel transform.
and applying a second Hankel transform.
 = 50 µm. (a) Ordinary, (b) zone-doubled, (c) zone-filled and (d) four-level staircase FZP geometries are considered. A photon energy of 6.2 keV, i.e. wavelength of 0.2 nm, is assumed.
= 50 µm. (a) Ordinary, (b) zone-doubled, (c) zone-filled and (d) four-level staircase FZP geometries are considered. A photon energy of 6.2 keV, i.e. wavelength of 0.2 nm, is assumed.
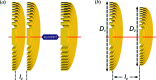
 can be stacked in the near-field to obtain an equivalent thicker structure and to achieve a substantial increase in diffraction efficiency. (b) The close proximity requirement on the two stacked FZPs can be relaxed by adjusting the diameter,
can be stacked in the near-field to obtain an equivalent thicker structure and to achieve a substantial increase in diffraction efficiency. (b) The close proximity requirement on the two stacked FZPs can be relaxed by adjusting the diameter,  , of the second diffractive optical element.
, of the second diffractive optical element.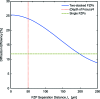
 = 100 nm, a zone height of
= 100 nm, a zone height of  = 500 nm each and a photon energy of 6.2 keV. As the separation distance
= 500 nm each and a photon energy of 6.2 keV. As the separation distance  increases, the diffraction efficiency of the two stacked FZPs decreases. The diffraction efficiency of a single ordinary FZP with the same parameters is shown for comparison.
increases, the diffraction efficiency of the two stacked FZPs decreases. The diffraction efficiency of a single ordinary FZP with the same parameters is shown for comparison.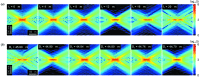
 = 25 nm. (a) When two FZPs of identical diameter,
= 25 nm. (a) When two FZPs of identical diameter,  = 45 µm, are stacked, the separation distance required for an acceptable focal spot shape is below
= 45 µm, are stacked, the separation distance required for an acceptable focal spot shape is below  = 10 µm. (b) The separation distance can be relaxed by adjusting the diameter,
= 10 µm. (b) The separation distance can be relaxed by adjusting the diameter,  , of the second FZP. For a separation distance of
, of the second FZP. For a separation distance of  = 25 µm an optimal focus profile is recovered for a diameter
= 25 µm an optimal focus profile is recovered for a diameter  = 44.8 µm.
= 44.8 µm.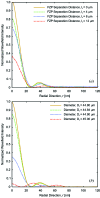
 = 25 nm. (a) With two FZPs of identical diameter,
= 25 nm. (a) With two FZPs of identical diameter,  = 45 µm, the focal spot is distorted by increasing their separation distance,
= 45 µm, the focal spot is distorted by increasing their separation distance,  . (b) For a chosen separation distance of
. (b) For a chosen separation distance of  = 25 µm, the optimal focal spot is recovered when the diameter of the second FZP is adjusted to
= 25 µm, the optimal focal spot is recovered when the diameter of the second FZP is adjusted to  = 44.8 µm.
= 44.8 µm.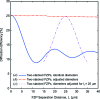
 = 20 nm and photon energy of 6.2 keV. (a) The diffraction efficiency decreases rapidly as a function of the separation distance
= 20 nm and photon energy of 6.2 keV. (a) The diffraction efficiency decreases rapidly as a function of the separation distance  when the two stacked FZPs have identical diameters. (b) The diffraction efficiency is kept constant when the diameter of the second FZP is optimized for every separation distance. (c) The diffractive efficiency for an experimentally realisable system in which the second FZP has a diameter adjusted for a separation distance of
when the two stacked FZPs have identical diameters. (b) The diffraction efficiency is kept constant when the diameter of the second FZP is optimized for every separation distance. (c) The diffractive efficiency for an experimentally realisable system in which the second FZP has a diameter adjusted for a separation distance of  = 25 µm.
= 25 µm.Similar articles
-
Efficient focusing of 8 keV X-rays with multilayer Fresnel zone plates fabricated by atomic layer deposition and focused ion beam milling.J Synchrotron Radiat. 2013 May;20(Pt 3):433-40. doi: 10.1107/S0909049513006602. Epub 2013 Apr 9. J Synchrotron Radiat. 2013. PMID: 23592622 Free PMC article.
-
Sharp-focusing Bragg-Fresnel zone plate with Laue diffraction geometry.J Synchrotron Radiat. 2006 Jul;13(Pt 4):343-5. doi: 10.1107/S0909049506018449. Epub 2006 Jun 15. J Synchrotron Radiat. 2006. PMID: 16799226
-
Fresnel zone plate stacking in the intermediate field for high efficiency focusing in the hard X-ray regime.Opt Express. 2014 Nov 17;22(23):28142-53. doi: 10.1364/OE.22.028142. Opt Express. 2014. PMID: 25402054
-
Ultra-high resolution zone-doubled diffractive X-ray optics for the multi-keV regime.Opt Express. 2011 Jan 3;19(1):175-84. doi: 10.1364/OE.19.000175. Opt Express. 2011. PMID: 21263555
-
Imaging cellular architecture with X-rays.Curr Opin Struct Biol. 2010 Oct;20(5):623-31. doi: 10.1016/j.sbi.2010.08.008. Epub 2010 Sep 24. Curr Opin Struct Biol. 2010. PMID: 20869868 Free PMC article. Review.
Cited by
-
Trapezoid-kinoform zone plate lens - a solution for efficient focusing in hard X-ray optics.J Synchrotron Radiat. 2022 Mar 1;29(Pt 2):386-392. doi: 10.1107/S1600577522000893. Epub 2022 Feb 15. J Synchrotron Radiat. 2022. PMID: 35254301 Free PMC article.
-
X-ray nanoprobes and diffraction-limited storage rings: opportunities and challenges of fluorescence tomography of biological specimens.J Synchrotron Radiat. 2014 Sep;21(Pt 5):1031-47. doi: 10.1107/S160057751401621X. Epub 2014 Aug 27. J Synchrotron Radiat. 2014. PMID: 25177992 Free PMC article.
-
More are better, but the details matter: combinations of multiple Fresnel zone plates for improved resolution and efficiency in X-ray microscopy.J Synchrotron Radiat. 2018 Jul 1;25(Pt 4):1048-1059. doi: 10.1107/S1600577518007208. Epub 2018 Jun 17. J Synchrotron Radiat. 2018. PMID: 29979166 Free PMC article.
-
An achromatic X-ray lens.Nat Commun. 2022 Mar 14;13(1):1305. doi: 10.1038/s41467-022-28902-8. Nat Commun. 2022. PMID: 35288546 Free PMC article.
References
-
- Aristov, V., Isoyan, A., Kohn, V., Kuyumchyam, A., Shulakov, E., Snigirev, A. & Snigireva, I. (2007). Nucl. Instrum. Methods Phys. Res. A, 575, 2007.
-
- Attwood, D. (2000). Soft X-rays and Extreme Ultraviolet Radiation. Cambridge University Press.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

