Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Apr 10;8(4):e61006.
doi: 10.1371/journal.pone.0061006. Print 2013.

Identifying communities and key vertices by reconstructing networks from samples

Bowen Yan  1 , Steve Gregory
Affiliations

Identifying communities and key vertices by reconstructing networks from samples

Bowen Yan et al. PLoS One. .

Abstract

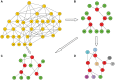
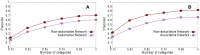
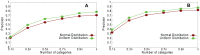
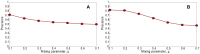
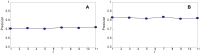
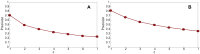
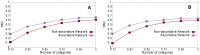
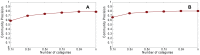
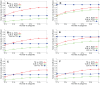
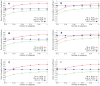
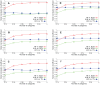
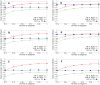
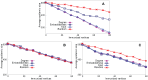
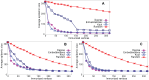
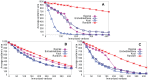
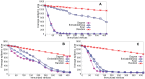
Sampling techniques such as Respondent-Driven Sampling (RDS) are widely used in epidemiology to sample "hidden" populations, such that properties of the network can be deduced from the sample. We consider how similar techniques can be designed that allow the discovery of the structure, especially the community structure, of networks. Our method involves collecting samples of a network by random walks and reconstructing the network by probabilistically coalescing vertices, using vertex attributes to determine the probabilities. Even though our method can only approximately reconstruct a part of the original network, it can recover its community structure relatively well. Moreover, it can find the key vertices which, when immunized, can effectively reduce the spread of an infection through the original network.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. Underlying network, samples, and reconstructed network.
A. Underlying network. B. Sample paths, with respondents in red and friends in green. C. True network. D. Reconstructed network: green vertices represent incorrectly coalesced pairs.
Figure 2
Figure 2. Performance of our method.
Precision, for varying g, on assortative and non-assortative LFR networks with normal distribution with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, and c max = 20. A. Random Path Method. B. High-degree Path Method.
Figure 3
Figure 3. Performance of our method.
Precision, for normal distribution and uniform distribution of vertex attributes, on non-assortative LFR networks with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, and c max = 20. A. Random Path Method. B. High-degree Path Method.
Figure 4
Figure 4. Performance of our method.
Precision, varying μ on non-assortative LFR networks with normal distribution with n = 1460, 〈k〉 = 20, k max = 30, τ 1 = 3, τ 2 = 1, c min = 10, c max = 20, and g = n. A. Random Path Method. B. High-degree Path Method.
Figure 5
Figure 5. Performance of our method.
Precision, varying f on non-assortative LFR networks with normal distribution with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, c max = 20, and g = n. A. Random Path Method. B. High-degree Path Method.
Figure 6
Figure 6. Performance of our method.
Precision, varying c on non-assortative LFR networks with normal distribution, with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, c max = 20, and g = n. A. Random Path Method. B. High-degree Path Method.
Figure 7
Figure 7. Comparison of partitions obtained in true network and reconstructed network.
Normalized Mutual Information, varying g, with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, and c max = 20. A. Random Path Method. B. High-degree Path Method.
Figure 8
Figure 8. Comparison of partitions obtained in underlying network and reconstructed network.
Community precision, varying g, with n = 1460, 〈k〉 = 20, k max = 30, μ = 0.1, τ 1 = 3, τ 2 = 1, c min = 10, and c max = 20. A. Random Path Method. B. High-degree Path Method.
Figure 9
Figure 9. Rank correlations for Email network.
A. Degree (RPM). B. k out (RPM). C. Embeddedness (RPM). D. Degree (HPM). E. k out (HPM). F. Embeddedness (HPM).
Figure 10
Figure 10. Rank correlations for Blogs network.
A. Degree (RPM). B. k out (RPM). C. Embeddedness (RPM). D. Degree (HPM). E. k out (HPM). F. Embeddedness (HPM).
Figure 11
Figure 11. Rank correlations for CA-GrQc network.
A. Degree (RPM). B. k out (RPM). C. Embeddedness (RPM). D. Degree (HPM). E. k out (HPM). F. Embeddedness (HPM).
Figure 12
Figure 12. Rank correlations for Erdös1997 network.
A. Degree (RPM). B. k out (RPM). C. Embeddedness (RPM). D. Degree (HPM). E. k out (HPM). F. Embeddedness (HPM).
Figure 13
Figure 13. Performance of four strategies on controlling disease in Email network.
Effect on epidemic size, varying number of immunized vertices. A. Immunizing top-ranked vertices in underlying network. B. Immunizing top-ranked vertices in reconstructed network: Random Path Method. C. Immunizing top-ranked vertices in reconstructed network: High-degree Path Method.
Figure 14
Figure 14. Performance of four strategies on controlling disease in Blogs network.
Effect on epidemic size, varying number of immunized vertices. A. Immunizing top-ranked vertices in underlying network. B. Immunizing top-ranked vertices in reconstructed network: Random Path Method. C. Immunizing top-ranked vertices in reconstructed network: High-degree Path Method.
Figure 15
Figure 15. Performance of four strategies on controlling disease in CA-GrQc network.
Effect on epidemic size, varying number of immunized vertices. A. Immunizing top-ranked vertices in underlying network. B. Immunizing top-ranked vertices in reconstructed network: Random Path Method. C. Immunizing top-ranked vertices in reconstructed network: High-degree Path Method.
Figure 16
Figure 16. Performance of four strategies on controlling disease in Erdös1997 network.
Effect on epidemic size, varying number of immunized vertices. A. Immunizing top-ranked vertices in underlying network. B. Immunizing top-ranked vertices in reconstructed network: Random Path Method. C. Immunizing top-ranked vertices in reconstructed network: High-degree Path Method.
Figure 17
Figure 17. Performance of degree and k out properties in controlling disease in real-world networks.
Effect on epidemic size, varying the size of the reconstructed network. (a) Blogs (RPM). (b) Erdös1997 (RPM). (c) Blogs (HPM). (d) Erdös1997 (HPM).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Lü L, Zhou T (2011) Link prediction in complex networks: a survey. Physica A 390: 1150–1170.
    1. Leskovec J, Huttenlocher D, Kleinberg J (2010) Predicting positive and negative links in online social networks. In: WWW 2010: Proceedings of the 19th International Conference on World Wide Web. Raleigh, North Carolina, USA, pp 641–650.
    1. Guo F, Yang Z, Zhou T (2012) Predicting link directions via a recursive subgraph-based ranking. Available: arXiv 1206.2199.
    1. Miller JC (2009) Spread of infectious diseases through clustered populations. J. R. Soc. Interface 6: 1121–1134. - PMC - PubMed
    1. Salathé M, Jones JH (2010) Dynamics and control of diseases in networks with community structure. PLoS Comput. Biol 6: e1000736. - PMC - PubMed

Publication types

LinkOut - more resources