Stem cell control, oscillations, and tissue regeneration in spatial and non-spatial models

Abstract

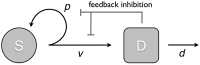
Normal human tissue is organized into cell lineages, in which the highly differentiated mature cells that perform tissue functions are the end product of an orderly tissue-specific sequence of divisions that start with stem cells or progenitor cells. Tissue homeostasis and effective regeneration after injuries requires tight regulation of these cell lineages and feedback loops play a fundamental role in this regard. In particular, signals secreted from differentiated cells that inhibit stem cell division and stem cell self-renewal are important in establishing control. In this article we study in detail the cell dynamics that arise from this control mechanism. These dynamics are fundamental to our understanding of cancer, given that tumor initiation requires an escape from tissue regulation. Knowledge on the processes of cellular control can provide insights into the pathways that lead to deregulation and consequently cancer development.

Keywords: cancer; cell linage control; mathematical models; tissue regeneration; tissue stability.

Figure 1

Model of tissue regulation with feedback loops. S represents the stem cell population and D the differentiated cell population. Stem cells divide at a rate v; this results in either two daughter stem cells with probability p; or two differentiated cells with probability 1 − p. Differentiated cells die at rate d. The rate of cell division and the probability of self-renewal are decreasing functions of the number of differentiated cells [equation (1)].

Figure 2

(A,B) Cell population with one feedback loop. (A) The trajectories oscillate toward steady state values (dotted line). Parameters, p₀ = 0.6, d = 0.1, g = 0.001, S(0) = 1, D(0) = 0. (B) If there is only one feedback loop the maximum self-renewal probability must be very close to 0.5 to ensure that the trajectories approach the steady states monotonically. In this subfigure d and g are the same as in (A) but p₀ = 0.513. (C,D) cell population with two feedback loops. (C) The steady state number of differentiated cells depends only p₀ and g and is independent of feedback on the division rates. The steady state number of stem cells increases when the number of feedback loops increase from one to two. The addition of feedback in the division rate dampens or altogether eliminates the oscillations. (D) Fitting fixed steady state values of stem cells and differentiated cells values with different levels of feedback inhibition in the division rate. The stronger the feedback signal in the division rate the smoother the transition the equilibrium transition to equilibrium.

Figure 3

(A,B) Cell population with one feedback loop. The stochastic simulation is shown in red for differentiated cells and green for stem cells. The ode is shown in blue for differentiated cells and black for stem cells. Parameters in (A) p₀ = 0.6, d = 0.1, g = 0.0001, h = 0, S(0) = 10, D(0) = 0. Parameters in (B) p₀ = 0.52, d = 0.2, g = 0.0001, h = 0, S(0) = 40, D(0) = 0. (C) Cell population with two feedback loops. Feedback in the division rate dampens oscillations. Parameters are the same as in (A) with the exception h = 0.001. (D) Sufficient conditions for the survival of the population in the ode model. Let us call the curve in the graph y($\stackrel{⌣}{D}$). Then for any set of parameters that satisfy (2p⁰ − 1)/g = $\stackrel{⌣}{D}$, p⁰ (0.5, 0.9) and the steady state fraction of stem cells f $\underset{¯}{\underset{¯}{>}}$y($\stackrel{⌣}{D}$), the initial conditions S(0) = 1, D(0) = 0 guarantee the survival of the population. For example, for all $\stackrel{⌣}{D}$ $\underset{¯}{\underset{¯}{>}}$ 10³ if p₀ $\underset{¯}{\underset{¯}{<}}$ 0.9 and the steady state fraction of stem cells f $\underset{¯}{\underset{¯}{>}}$ 0.064 survival is guaranteed for any level of feedback on the division rate. (These conditions are sufficient but not necessary.)

Figure 4

(A) Example of the spatial arrangement of the cell population in three dimensions. Differentiated cells are shown in blue and stem cells in red. (B) Cell count of differentiated cells vs. time. The blue line was computed using the ode model, the red line is the expected cell count in the spatial model. (C) Cell count of stem cells. Results form the ode (black) and expected cell count in spatial-dimensional model (green). The expected number of cells is in the spatial model is shown in blue. (D) Expected fraction of stem cells that are free in the three-dimensional model. Parameters in all figures are: p₀ = 0.7, v₀ = 0.2, g = 2 × 10⁵, β = 1, and d = 0.0025.