Phase transition in the economically modeled growth of a cellular nervous system

Abstract

Spatially embedded complex networks, such as nervous systems, the Internet, and transportation networks, generally have nontrivial topological patterns of connections combined with nearly minimal wiring costs. However, the growth rules shaping these economical tradeoffs between cost and topology are not well understood. Here, we study the cellular nervous system of the nematode worm Caenorhabditis elegans, together with information on the birth times of neurons and on their spatial locations. We find that the growth of this network undergoes a transition from an accelerated to a constant increase in the number of links (synaptic connections) as a function of the number of nodes (neurons). The time of this phase transition coincides closely with the observed moment of hatching, when development switches metamorphically from oval to larval stages. We use graph analysis and generative modeling to show that the transition between different growth regimes, as well as its coincidence with the moment of hatching, may be explained by a dynamic economical model that incorporates a tradeoff between topology and cost that is continuously negotiated and renegotiated over developmental time. As the body of the animal progressively elongates, the cost of longer-distance connections is increasingly penalized. This growth process regenerates many aspects of the adult nervous system's organization, including the neuronal membership of anatomically predefined ganglia. We expect that similar economical principles may be found in the development of other biological or manmade spatially embedded complex systems.

Keywords: C. elegans; connectome; generative model; neurodevelopment; spatial network.

Fig. 1.

Development of the C. elegans nervous system. (A) C. elegans reaches maturity roughly 63 h after fertilization. During this time, its body length increases from to (–24). (B) In the adult hermaphrodite worm, more than of the neurons are located in the head and about are found in the tip of the tail (based on data modified according to ref. , axis arbitrarily centered such that the origin is at the base of the head). Neurons are colored by ganglion membership (16): anterior [A], dorsal [B], lateral [C], ventral [D], retrovesicular [E], ventral cord [G], posterior lateral [F], preanal [H], dorsorectal [J], and lumbar [K]. (C) The total number of neurons (N, solid black), and connections (K, dashed blue), grows rapidly between 250 and 500 min after fertilization. Another burst of neurogenesis is observed at the end of the L1 larval stage (using data from ref. 17). (D) Plotting the number of synapses as a function of the number of neurons (yellow ●) reveals the presence of a phase transition. Before hatching, K grows as (solid blue line), whereas after hatching, K grows linearly with N (dashed green line). (Inset) Plot of the average nodal degree vs. N.

Fig. 2.

Modeling network growth. (A) The linear preferential attachment model (BA, blue ■) fails to reproduce the biphasic growth observed (solid line). (B) In the BAG model (magenta ■) and the HAG model (dashed blue line), the average node degree increases linearly with the size of the network. 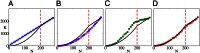(C) The ESG model (green ■) exhibits a biphasic behavior, yielding a transition from quadratic to nearly linear growth at , but fails to capture the details of the observed growth. (D) The ESTG model (red ■) accurately reproduces the details of the biphasic growth trajectory; for example, the inflection point of the modeled developmental curve corresponds closely to the moment of metamorphosis (hatching). The red dashed line in each panel indicates the number of nodes at the time of hatching . The SE of each growth curve is smaller than the size of the symbols used to plot it and is not reported.

Fig. 3.

Local and mesoscopic network structures. (A) The distributions of node degree (Left, blue), connection distance (Center, red), and node efficiency (Right, orange) of model-generated networks closely match those observed in the C. elegans neuronal network (shown in gray). (B) This panel shows how the average node degree (Upper) and the average node efficiency (Lower) vary along the length of the C. elegans body (solid black lines) and in networks generated using the ESTG model (red dashed lines). (C) Networks created using the ESTG model (Right) also reproduce the pattern of intra- and interganglia connections observed in C. elegans (Left). Brighter colors indicate higher connection density; letters A–K denote neuronal ganglia as defined in legend to Figure 1.