Microcavity controlled coupling of excitonic qubits
- PMID: 23612288
- PMCID: PMC3644086
- DOI: 10.1038/ncomms2764
Microcavity controlled coupling of excitonic qubits
Abstract
Controlled non-local energy and coherence transfer enables light harvesting in photosynthesis and non-local logical operations in quantum computing. This process is intuitively pictured by a pair of mechanical oscillators, coupled by a spring, allowing for a reversible exchange of excitation. On a microscopic level, the most relevant mechanism of coherent coupling of distant quantum bits--like trapped ions, superconducting qubits or excitons confined in semiconductor quantum dots--is coupling via the electromagnetic field. Here we demonstrate the controlled coherent coupling of spatially separated quantum dots via the photon mode of a solid state microresonator using the strong exciton-photon coupling regime. This is enabled by two-dimensional spectroscopy of the sample's coherent response, a sensitive probe of the coherent coupling. The results are quantitatively understood in a rigorous description of the cavity-mediated coupling of the quantum dot excitons. This mechanism can be used, for instance in photonic crystal cavity networks, to enable a long-range, non-local coherent coupling.
Figures
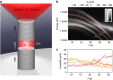

 , E2 for
, E2 for  ). (b) Transitions emitting FWM after the arrival of the second pulse.
). (b) Transitions emitting FWM after the arrival of the second pulse.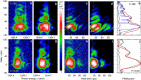
 , measured (a,f) and predicted (b,g), on a logarithmic colour scale over four orders of magnitude. Time-resolved FWM power
, measured (a,f) and predicted (b,g), on a logarithmic colour scale over four orders of magnitude. Time-resolved FWM power  , measured (c,h) and predicted (d,i) over three orders. (e,j) Time-integrated FWM power
, measured (c,h) and predicted (d,i) over three orders. (e,j) Time-integrated FWM power  , measured (black circles) and predicted (red line), and measured
, measured (black circles) and predicted (red line), and measured  (blue triangles). The noise of
(blue triangles). The noise of  is given as open circles.
is given as open circles.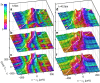
 meV.
meV.  measured and phase corrected (a) and predicted with (b) and without (c) phase correction. The amplitude is given as height, while the phase is given as hue of the surface colour, as indicated. The white line shows the diagonal
measured and phase corrected (a) and predicted with (b) and without (c) phase correction. The amplitude is given as height, while the phase is given as hue of the surface colour, as indicated. The white line shows the diagonal  on the surface. (d–f) As (a–c), but showing the post-selected
on the surface. (d–f) As (a–c), but showing the post-selected  . Different representations of the data are shown in Supplementary Figs S10 and S11.
. Different representations of the data are shown in Supplementary Figs S10 and S11.References
-
- Majer J. et al.. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447 (2007). - PubMed
-
- Schoelkopf R. J., Girvin S. M. Wiring up quantum systems. Nature 451, 664–669 (2008). - PubMed
-
- Leek P. J. et al.. Using sideband transitions for two-qubit operations in superconducting circuits. Phys. Rev. B 79, 180511R (2009).
-
- Chow J. M. et al.. Simple all-microwave entangling gate for fixed-frequency superconducting qubits. Phys. Rev. Lett. 107, 080502 (2011). - PubMed
-
- Reithmaier J. P. et al.. Strong coupling in a single quantum dot-semiconductor microcavity system. Nature 432, 197–200 (2004). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

