High-resolution nanomechanical analysis of suspended electrospun silk fibers with the torsional harmonic atomic force microscope

Abstract

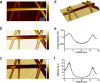
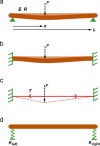
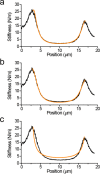
Atomic force microscopes have become indispensable tools for mechanical characterization of nanoscale and submicron structures. However, materials with complex geometries, such as electrospun fiber networks used for tissue scaffolds, still pose challenges due to the influence of tension and bending modulus on the response of the suspended structures. Here we report mechanical measurements on electrospun silk fibers with various treatments that allow discriminating among the different mechanisms that determine the mechanical behavior of these complex structures. In particular we were able to identify the role of tension and boundary conditions (pinned versus clamped) in determining the mechanical response of electrospun silk fibers. Our findings show that high-resolution mechanical imaging with torsional harmonic atomic force microscopy provides a reliable method to investigate the mechanics of materials with complex geometries.

Keywords: atomic force microscopy; nanomechanical characterization; silk fibers; tissue scaffolds; torsional harmonic cantilevers.

Figure 1

Topography of electrospun silk fibers on a glass substrate. The 3-D image is rendered according to the local height measured by the atomic force microscope. The scan size is 20 × 20 µm². The fibers form a mesh-like network. Branches between intersections occasionally form suspended fibers, allowing us to investigate their mechanical behavior.

Figure 2

Simultaneously measured topography (a), elastic modulus (b), and stiffness (c) maps obtained from electrospun silk fibers. Color bars in (a–c) correspond to the ranges in height (0–1.8 µm), elastic modulus (10 MPa to 10 GPa, mapped logarithmically), and stiffness (0–5 N/m). The horizontal fiber appears to be suspended above the glass substrate. A 3-D rendering of the topography image is given in (d). The fiber is suspended between positions indicated by arrows in (d). This image is colored according to the local spring constant. Both the elastic modulus and stiffness maps show gradual variations across the suspended silk fiber. Line profiles of elastic modulus and stiffness across the dashed line in (b) are given in (e) and (f), respectively. While the local elastic modulus of the silk fiber is likely to be constant across the length of the fiber, the values in (e) show significant variation. This is because the elastic modulus values in (b,e) are calculated by the DMT contact-mechanics model, which does not take the suspended geometry of the fiber into account. Therefore, the regions of the elastic modulus image corresponding to suspended fibers are not reliable. These regions are better analyzed in the light of mechanical models describing the entire suspended structure by using the stiffness values in (c,f).

Figure 3

Illustration of possible mechanisms determining the local spring constant of suspended silk fibers. (a) “Pinned-end model” assumes that the fiber displacement is zero at the nodes; however, there is no constraint on its angle at the nodes. E elastic modulus, R is fiber radius, L is branch length. (b) “Clamped-end model” assumes that both the angle and displacement at the nodes are zero. (c) “Tension model” assumes the fiber has a built in tension T and negligible bending modulus. (d) “Suspended rigid rod model” assumes the nodes have finite spring constants K_left and K_right. Note that the spring constant according to the mechanism in (d) acts in series with the mechanisms in (a–c).

Figure 4

Curves described by equations for pinned end (a), clamped end (b), and tension (c) models fitted to the data. Values of the variables used for fitting are listed in Table 1.