A robustness study of parametric and non-parametric tests in model-based multifactor dimensionality reduction for epistasis detection

Abstract

Background: Applying a statistical method implies identifying underlying (model) assumptions and checking their validity in the particular context. One of these contexts is association modeling for epistasis detection. Here, depending on the technique used, violation of model assumptions may result in increased type I error, power loss, or biased parameter estimates. Remedial measures for violated underlying conditions or assumptions include data transformation or selecting a more relaxed modeling or testing strategy. Model-Based Multifactor Dimensionality Reduction (MB-MDR) for epistasis detection relies on association testing between a trait and a factor consisting of multilocus genotype information. For quantitative traits, the framework is essentially Analysis of Variance (ANOVA) that decomposes the variability in the trait amongst the different factors. In this study, we assess through simulations, the cumulative effect of deviations from normality and homoscedasticity on the overall performance of quantitative Model-Based Multifactor Dimensionality Reduction (MB-MDR) to detect 2-locus epistasis signals in the absence of main effects.

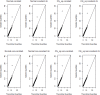
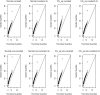
Methodology: Our simulation study focuses on pure epistasis models with varying degrees of genetic influence on a quantitative trait. Conditional on a multilocus genotype, we consider quantitative trait distributions that are normal, chi-square or Student's t with constant or non-constant phenotypic variances. All data are analyzed with MB-MDR using the built-in Student's t-test for association, as well as a novel MB-MDR implementation based on Welch's t-test. Traits are either left untransformed or are transformed into new traits via logarithmic, standardization or rank-based transformations, prior to MB-MDR modeling.

Results: Our simulation results show that MB-MDR controls type I error and false positive rates irrespective of the association test considered. Empirically-based MB-MDR power estimates for MB-MDR with Welch's t-tests are generally lower than those for MB-MDR with Student's t-tests. Trait transformations involving ranks tend to lead to increased power compared to the other considered data transformations.

Conclusions: When performing MB-MDR screening for gene-gene interactions with quantitative traits, we recommend to first rank-transform traits to normality and then to apply MB-MDR modeling with Student's t-tests as internal tests for association.

Figure 1

Group comparison test maintaining adequate Type 1 error control, when group sizes are unequal. Legend: When several tests are listed, they are listed from most (top) to least (bottom) powerful. The tests in a square box and blue font should be avoided in MB-MDR due to reasons mentioned next to them.

Figure 2

Density plots for original trait (panel A) and rank transformed traits (panel B) for one simulated data replicate with epistatic variance 10%. Legend: Numbers as they appear with color lines in the legend: 1=normal constant variance, 2=normal non-constant variance, 3=chi-square constant variance, 4=chi-square non-constant variance. Wild-type individuals (homozygous for the major allele) are coded as 0, heterozygous individuals as 1, and individuals homozygous for the minor allele as 2. Figures in brackets represent sample sizes for the multi-locus genotype cells.

Figure 3

Qq-plots of observed squared Student’s t- test values for association between the multi-locus genotype combination cell 0-0 versus the pooled remaining multi-locus genotypes, for normal and chi-squared trait distributions or non-transformed and rank-transformed to normal data. Each time, one replicate with epistatic variance 10% is considered and F-statistics are pooled for all SNP pairs over the 999 permutations. A generated F-distribution according to F(1,498) is taken as the reference.

Figure 4

Qq-plots of MB-MDR step 2 test values (squared Student’s t), for normal and chi-squared trait distributions, and non-transformed or rank-transformed to normal data. For each setting, one replicate with epistatic variance 10% is considered and F-statistics are pooled for all SNP pairs over the 999 permutations. A theoretical F-distribution according to F (1,498) is taken as the reference.

Figure 5

Scatter plot matrices of MB-MDR multiple testing corrected p-values for the causal SNP pair for a variety of a priori data transformations. Only MB-MDR results with Student’s t testing for associations are shown. The epistatic contribution to the trait variance is set to 10%. Legend: Different scenario’s of trait distribution are considered: normal traits and homogeneity (panel A); normal traits and heteroscedasticity (panel B); chi-squared distributed traits and homogeneity (panel C); chi-squared distributed traits and variance heterogeneity (panel D).