Design of multishell sampling schemes with uniform coverage in diffusion MRI
- PMID: 23625329
- PMCID: PMC5381389
- DOI: 10.1002/mrm.24736
Design of multishell sampling schemes with uniform coverage in diffusion MRI
Abstract
Purpose: In diffusion MRI, a technique known as diffusion spectrum imaging reconstructs the propagator with a discrete Fourier transform, from a Cartesian sampling of the diffusion signal. Alternatively, it is possible to directly reconstruct the orientation distribution function in q-ball imaging, providing so-called high angular resolution diffusion imaging. In between these two techniques, acquisitions on several spheres in q-space offer an interesting trade-off between the angular resolution and the radial information gathered in diffusion MRI. A careful design is central in the success of multishell acquisition and reconstruction techniques.
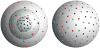
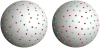
Methods: The design of acquisition in multishell is still an open and active field of research, however. In this work, we provide a general method to design multishell acquisition with uniform angular coverage. This method is based on a generalization of electrostatic repulsion to multishell.
Results: We evaluate the impact of our method using simulations, on the angular resolution in one and two bundles of fiber configurations. Compared to more commonly used radial sampling, we show that our method improves the angular resolution, as well as fiber crossing discrimination.
Discussion: We propose a novel method to design sampling schemes with optimal angular coverage and show the positive impact on angular resolution in diffusion MRI.
Copyright © 2012 Wiley Periodicals, Inc.
Figures

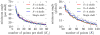
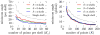

References
-
- Le Bihan D, Breton E. Imagerie De diffusion it in vivo par rsonnance magntique nuclaire. CR Acad Sci. 1985;301:1109–1112.
-
- Taylor D, Bushell M. The spatial mapping of translational diffusion coefficients by the NMR imaging technique. Phys Med Biol. 1985;30:345–349. - PubMed
-
- Merboldt K, Hanicke W, Frahm J. Self-diffusion NMR imaging using stimulated echoes. J Magn Reson. 1985;64:479–486.
-
- Jones DK, editor. Diffusion MRI: theory, methods, and applications. New York: Oxford University Press; 2010.
-
- Johansen-Berg H, Behrens TE, editors. Diffusion MRI: from quantitative measurement to in-vivo neuroanatomy. London: Academic Press; 2009.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

