Perceptual decision making "through the eyes" of a large-scale neural model of v1

Abstract

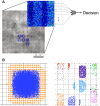
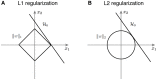
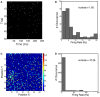
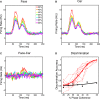
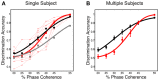
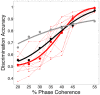
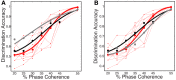
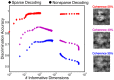
Sparse coding has been posited as an efficient information processing strategy employed by sensory systems, particularly visual cortex. Substantial theoretical and experimental work has focused on the issue of sparse encoding, namely how the early visual system maps the scene into a sparse representation. In this paper we investigate the complementary issue of sparse decoding, for example given activity generated by a realistic mapping of the visual scene to neuronal spike trains, how do downstream neurons best utilize this representation to generate a "decision." Specifically we consider both sparse (L1-regularized) and non-sparse (L2 regularized) linear decoding for mapping the neural dynamics of a large-scale spiking neuron model of primary visual cortex (V1) to a two alternative forced choice (2-AFC) perceptual decision. We show that while both sparse and non-sparse linear decoding yield discrimination results quantitatively consistent with human psychophysics, sparse linear decoding is more efficient in terms of the number of selected informative dimension.

Keywords: computational modeling; decision making; neuronal network; sparse coding.

Figure 1

The stimulus set for the 2-AFC perceptual decision making task. (A) Shown are 12 face and 12 car images at phase coherence 55%. (B) One sample face and one sample car image, at phase coherences varying from 20 to 55%. (C) Design and timing of the simulated psychophysics experiment for the model.

Figure 2

Summary of the model architecture. (A) The model is comprises of the encoding and decoding components. (B) Architecture of the V1 model, where receptive fields and LGN axon targets are viewed in the visual space (left) and cortical space (right). Details can be found in Wielaard and Sajda (2006a).

Figure 3

A schematic illustration of how different regularization terms lead to sparse and non-sparse solutions in the linear classifier. (A) L1 regularization corresponds to the diamond shaped ball centered around the origin. (B) L2 regularization corresponds to the spherical ball centered around the origin.

Figure 4

(A) Spike trains of one example neuron over 50 trials, simulated for a face stimulus. (B) Distribution of firing rates has a kurtosis of 1.65, indicative of temporal sparseness. (C) Spatial distribution of instantaneous firing rates over all neurons in the network. Firing rates are computed at 50 ms post-stimulus for one trial. (D) Distribution of firing rates has a kurtosis of 10.26.

Figure 5

(A) Average response over all the model’s cortical neurons for all face stimuli. (B) Average response over all the Magnocortical neurons for all car stimuli. (C) Average response difference between face and car stimuli for the Magno system. (D) Neurometric curve by decoding spatially averaged firing rates for the V1 model (thick black curve) is plotted, together with the group average psychometric curve fitted across 10 subjects (thick red curve), and psychophysical performance of 10 individual subjects (thin dashed red lines).

Figure 6

(A) Spike trains from simulated neurons are aligned relative to stimulus onset. Words are constructed by binning spike trains using a given temporal bin width. (B) A spatio-temporal word represented as a matrix of size N neurons by 10 time bins, each time bin being 25 ms wide. Numbers indicate spike counts for bins with at least one spike. (C) A word represented as a vector of length N, computed using a single bin of size 250 ms.

Figure 7

(A) Simulated neurometric performance for one initialization of the V1 model. Shown are (black) neurometric curve constructed by decoding the full spatio-temporal word, D = 3.19, p = 0.53; (gray) neurometric curve constructed from a decoder that ignores dynamics, D = 52.26, p < 0.01. Also shown is (dashed red lines) the psychophysical performance of 10 human subjects, and (solid red curve) the group psychometric curve across 10 subjects. (B) Shown are (black) simulated neurometric performance averaged over five initializations of the model, together with (red) the average psychometric curve for the 10 human subjects. Error bars on both curves represent standard error. Likelihood ratio test yields D = 6.42, p = 0.17.

Figure 8

Decoding accuracy compared to a feedforward model. Comparison of psychometric and two neurometric curves, one for sparse linear decoding of activity generated by our dynamical V1 model (black curved – same as Figure 7A, D = 3.19, p = 0.53;) the other for a sparse linear decoding of activity generated by the first layer of the feed forward HMAX model (gray curve; D = 48.26 (p < 0.01). Code for simulating HMAX feedforward model is freely available from http://cbcl.mit.edu/jmutch/cns/hmax/doc/

Figure 9

Comparison of several decoding strategies. (A) Two decoding strategies: (black) train and test at each coherence independently, D = 3.19, P = 0.53; (gray) train at the highest coherence and test at each coherence, D = 12.88, P = 0.01. Both are trained as sparse decoders. (B) Sparse and non-sparse decoding strategies: (black) sparse decoder, D = 3.19, P = 0.53; (gray) non-sparse decoder each with the same amount of regularization, D = 3.66, P = 0.45. Both are trained on each coherence independently. Also shown are (dashed red lines) the psychophysical performance of 10 human subjects; (solid red curve) the group psychometric curve across 10 subjects.

Figure 10

Discrimination accuracy for both sparse and non-sparse decoding strategies. Decoding is shown for three different coherence levels while sweeping the hyperparameter that controls the amount of regularization. Sparse decoding always yields fewer informative dimensions while also having greater discrimination accuracy for each of the three coherence levels.

Figure 11

(A) Number of informative dimensions decrease as the task becomes easier. (B) Number of informative neurons decreases as the task becomes easier. (C) Difference between the number of informative dimensions and the number of informative neurons.

Figure 12

(A) Example of images at three coherence levels. (B) Spatial distribution of neurons selected by the decoder. Shown are neurons in the cortical space, where selected neurons are indicated in black. (C) Temporal windows selected by the decoder together with their corresponding weights. (D) Chronometric function indicating the time needed by the decoder to accumulate evidence in the network dynamics. (E) Behavioral chronometric functions derived from human psychophysics.