Dynamical models explaining social balance and evolution of cooperation
- PMID: 23634204
- PMCID: PMC3636264
- DOI: 10.1371/journal.pone.0060063
Dynamical models explaining social balance and evolution of cooperation
Abstract
Social networks with positive and negative links often split into two antagonistic factions. Examples of such a split abound: revolutionaries versus an old regime, Republicans versus Democrats, Axis versus Allies during the second world war, or the Western versus the Eastern bloc during the Cold War. Although this structure, known as social balance, is well understood, it is not clear how such factions emerge. An earlier model could explain the formation of such factions if reputations were assumed to be symmetric. We show this is not the case for non-symmetric reputations, and propose an alternative model which (almost) always leads to social balance, thereby explaining the tendency of social networks to split into two factions. In addition, the alternative model may lead to cooperation when faced with defectors, contrary to the earlier model. The difference between the two models may be understood in terms of the underlying gossiping mechanism: whereas the earlier model assumed that an individual adjusts his opinion about somebody by gossiping about that person with everybody in the network, we assume instead that the individual gossips with that person about everybody. It turns out that the alternative model is able to lead to cooperative behaviour, unlike the previous model.
Conflict of interest statement
Figures
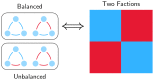

 , while the second row displays the results for
, while the second row displays the results for  . Each row contains from left to right: (1) an illustration of the model; (2) the random initial state; (3) the dynamics of the model; and (4) the final state to which the dynamics converge. Blue indicates positive entries, and red negative entries. Although the first model converges to a rank one matrix, it is not socially balanced. The second model does converge generically to social balance. The small bumps in the dynamics for
. Each row contains from left to right: (1) an illustration of the model; (2) the random initial state; (3) the dynamics of the model; and (4) the final state to which the dynamics converge. Blue indicates positive entries, and red negative entries. Although the first model converges to a rank one matrix, it is not socially balanced. The second model does converge generically to social balance. The small bumps in the dynamics for  are due to complex eigenvalues that show circular behaviour (see Fig. S1).
are due to complex eigenvalues that show circular behaviour (see Fig. S1).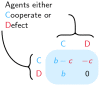

 than
than  . This implies that the model
. This implies that the model  is more viable against defectors, and has an evolutionary advantage compared to
is more viable against defectors, and has an evolutionary advantage compared to  . (B) The point b* at which the model
. (B) The point b* at which the model  has an evolutionary advantage against defectors (i.e. the fixation probability ρ >1/2) depends on the number of agents n. The condition for the model
has an evolutionary advantage against defectors (i.e. the fixation probability ρ >1/2) depends on the number of agents n. The condition for the model  to defeat defectors can be approximated by
to defeat defectors can be approximated by  , with β ≈ 1.72.
, with β ≈ 1.72.References
-
- Heider F (1946) Attitudes and Cognitive Organization. J Psychol 21: 107–112. - PubMed
-
- Harary F (1953) On the notion of balance of a signed graph. The Michigan Mathematical Journal 2: 143–146.
-
- Cartwright D, Harary F (1956) Structural balance: a generalization of Heider's theory. Psychol Rev 63: 277–293. - PubMed
-
- Doreian P, Mrvar A (1996) A partitioning approach to structural balance. Soc Networks 18: 149–168.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

