Minimum-norm cortical source estimation in layered head models is robust against skull conductivity error

Abstract

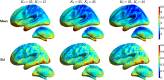
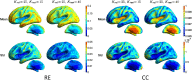
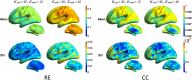
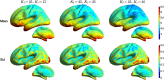
The conductivity profile of the head has a major effect on EEG signals, but unfortunately the conductivity for the most important compartment, skull, is only poorly known. In dipole modeling studies, errors in modeled skull conductivity have been considered to have a detrimental effect on EEG source estimation. However, as dipole models are very restrictive, those results cannot be generalized to other source estimation methods. In this work, we studied the sensitivity of EEG and combined MEG+EEG source estimation to errors in skull conductivity using a distributed source model and minimum-norm (MN) estimation. We used a MEG/EEG modeling set-up that reflected state-of-the-art practices of experimental research. Cortical surfaces were segmented and realistically-shaped three-layer anatomical head models were constructed, and forward models were built with Galerkin boundary element method while varying the skull conductivity. Lead-field topographies and MN spatial filter vectors were compared across conductivities, and the localization and spatial spread of the MN estimators were assessed using intuitive resolution metrics. The results showed that the MN estimator is robust against errors in skull conductivity: the conductivity had a moderate effect on amplitudes of lead fields and spatial filter vectors, but the effect on corresponding morphologies was small. The localization performance of the EEG or combined MEG+EEG MN estimator was only minimally affected by the conductivity error, while the spread of the estimate varied slightly. Thus, the uncertainty with respect to skull conductivity should not prevent researchers from applying minimum norm estimation to EEG or combined MEG+EEG data. Comparing our results to those obtained earlier with dipole models shows that general judgment on the performance of an imaging modality should not be based on analysis with one source estimation method only.

Keywords: Electroencephalography; Inverse problem; Magnetoencephalography; Minimum-norm estimation; Skull conductivity.

Fig. A1

Peak position error PPE (in centimeters) for EMEG with different inverse model conductivities. For further explanation, see the caption of Fig. 3.

Fig. A2

Spatial deviation (in centimeters) for EMEG as function of test model conductivity. For further explanation, see the caption of Fig. 3.

Fig. A3

Relative cortical area CA (in percents) for EMEG as function of test model conductivity. For further explanation, see the caption of Fig. 3.

Fig. 1

Relative error (RE) and correlation coefficient (CC) between EEG forward models computed with different skull conductivity contrasts K. The reference K is in all comparisons 25, while the test K is either 15 or 40. The larger and smaller plots show the lateral and medial views of the inflated brain surface, respectively.

Fig. 2

Relative error (RE) and correlation coefficient (CC) between EEG spatial filter vectors with different skull conductivity contrasts K. The reference K is in all comparisons 25, while the test K is either 15 or 40.

Fig. 3

Peak position error PPE (in centimeters) for different EEG inverse model conductivities. The forward solutions were computed with K = K_f = 25 and the inverse solutions with K = K_i of 15, 25, or 40. The pseudocolor plots show the population mean on the upper row and standard deviation on the lower row with all test conductivities (columns). The results with the reference model, computed with the same conductivities in the forward and inverse models, are in the middle column.

Fig. 4

Spatial deviation (in centimeters) for EEG as function of test model conductivity. Notice that the color scale for the mean does not start at zero. For further explanation, see the caption of Fig. 3.

Fig. 5

Relative cortical area CA (in percents) for EEG as function of test model conductivity. For further explanation, see the caption of Fig. 3.