Determination of the interfacial rheological properties of a poly(DL-lactic acid)-encapsulated contrast agent using in vitro attenuation and scattering

Abstract

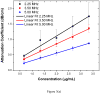
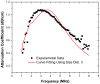
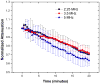
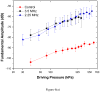
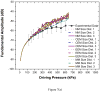
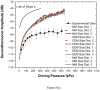
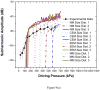
The stabilizing encapsulation of a microbubble-based ultrasound contrast agent (UCA) critically affects its acoustic properties. Polymers, which behave differently from materials commonly used (i.e., lipids or proteins) for monolayer encapsulation, have the potential for better stability and improved control of encapsulation properties. Air-filled microbubbles coated with poly(DL-lactic acid) (PLA) are characterized here using in vitro acoustic experiments and several models of encapsulation. The interfacial rheological properties of the encapsulation are determined according to each model using attenuation of ultrasound through a suspension of microbubbles. Then the model predictions are compared with scattered non-linear (sub- and second harmonic) responses. For this microbubble population (average diameter, 1.9 μm), the peak in attenuation measurement indicates a weighted-average resonance frequency of 2.5-3 MHz, which, in contrast to other encapsulated microbubbles, is lower than the resonance frequency of a free bubble of similar size (diameter, 1.9 μm). This apparently contradictory result stems from the extremely low surface dilational elasticity (around 0.01-0.07 N/m) and the reduced surface tension of the poly(DL-lactic acid) encapsulation, as well as the polydispersity of the bubble population. All models considered here are shown to behave similarly even in the non-linear regime because of the low surface dilational elasticity value. Pressure-dependent scattering measurements at two different excitation frequencies (2.25 and 3 MHz) revealed strongly non-linear behavior with 25-30 dB and 5-20 dB enhancements in fundamental and second-harmonic responses, respectively, for a contrast agent concentration of 1.33 μg/mL in the suspension. Sub-harmonic responses are registered above a relatively low generation threshold of 100-150 kPa, with up to 20 dB enhancement beyond that pressure. Numerical predictions from all models show good agreement with the experimentally measured fundamental response, but not with the experimental second-harmonic response. The characteristic features of sub-harmonic responses and the steady response beyond the threshold are matched well by model predictions. However, prediction of the threshold value depends on estimated properties and size distribution. The variation in size distribution from sample to sample leads to variation in estimates of encapsulation properties: the lowest estimated value for surface dilational viscosity better predicts the sub-harmonic threshold.

Figure 1

Schematic of the experimental setup for in vitro measurement of (a) attenuation (b) scattering.

Figure 1

Schematic of the experimental setup for in vitro measurement of (a) attenuation (b) scattering.

Figure 2

Size distribution of PLA shelled contrast microbubbles measured using DLS for three independent measurements.

Figure 3

(a) Attenuation coefficient at the central frequencies of the three transducers (2.25, 3.5, 5 MHz) as a function of bubble concentration (averaged over five different acquisitions). (b) Frequency dependent attenuation coefficient measured with three different transducers (with central frequencies 2.25, 3.5, 5 MHz) averaged over five different acquisitions.

Figure 3

(a) Attenuation coefficient at the central frequencies of the three transducers (2.25, 3.5, 5 MHz) as a function of bubble concentration (averaged over five different acquisitions). (b) Frequency dependent attenuation coefficient measured with three different transducers (with central frequencies 2.25, 3.5, 5 MHz) averaged over five different acquisitions.

Figure 4

Experimentally measured attenuation and prediction by the Newtonian model obtained during parameter estimation using sample 3 size distribution.

Figure 5

Normalized total attenuation coefficient with time. The data were averaged over five different acquisitions each collected continuously and averaged over consecutive 30 second intervals.

Figure 6

Experimentally measured scattered response from PLA microbubbles for two different excitation frequencies (2.25 MHz, 3.5 MHz): (a) Fundamental (b) Second harmonic and (c) Subharmonic. Control indicates data without any bubbles introduced.

Figure 6

Experimentally measured scattered response from PLA microbubbles for two different excitation frequencies (2.25 MHz, 3.5 MHz): (a) Fundamental (b) Second harmonic and (c) Subharmonic. Control indicates data without any bubbles introduced.

Figure 6

Experimentally measured scattered response from PLA microbubbles for two different excitation frequencies (2.25 MHz, 3.5 MHz): (a) Fundamental (b) Second harmonic and (c) Subharmonic. Control indicates data without any bubbles introduced.

Figure 7

Comparison of experimentally measured and predicted scattered fundamental response from different models for PLA bubbles using three different size distributions at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model.

Figure 7

Comparison of experimentally measured and predicted scattered fundamental response from different models for PLA bubbles using three different size distributions at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model.

Figure 8

Comparison of experimentally measured and predicted scattered second harmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. A line with a slope of 2 is also shown for comparison.

Figure 8

Comparison of experimentally measured and predicted scattered second harmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. A line with a slope of 2 is also shown for comparison.

Figure 9

Comparison of experimentally measured and predicted scattered subharmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. The curves for CEM and MM, size distribution 2, 2.25 MHz have thresholds too high to be seen here.

Figure 9

Comparison of experimentally measured and predicted scattered subharmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. The curves for CEM and MM, size distribution 2, 2.25 MHz have thresholds too high to be seen here.

Figure 10

Comparison of experimentally measured and predicted scattered subharmonic response from PLA bubbles with Newtonian Model with different size distributions and Sample 3 parameter values at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model.

Figure 10

Comparison of experimentally measured and predicted scattered subharmonic response from PLA bubbles with Newtonian Model with different size distributions and Sample 3 parameter values at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model.