The benefits of selecting phenotype-specific variants for applications of mixed models in genomics
- PMID: 23657357
- PMCID: PMC3648840
- DOI: 10.1038/srep01815
The benefits of selecting phenotype-specific variants for applications of mixed models in genomics
Abstract
Applications of linear mixed models (LMMs) to problems in genomics include phenotype prediction, correction for confounding in genome-wide association studies, estimation of narrow sense heritability, and testing sets of variants (e.g., rare variants) for association. In each of these applications, the LMM uses a genetic similarity matrix, which encodes the pairwise similarity between every two individuals in a cohort. Although ideally these similarities would be estimated using strictly variants relevant to the given phenotype, the identity of such variants is typically unknown. Consequently, relevant variants are excluded and irrelevant variants are included, both having deleterious effects. For each application of the LMM, we review known effects and describe new effects showing how variable selection can be used to mitigate them.
Figures
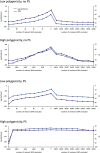
 (blue) and squared error (purple) averaged over the folds of cross validation are plotted as a function of the number of relevant SNPs randomly excluded (left) and number of irrelevant SNPs randomly included (right) in the RRM.
(blue) and squared error (purple) averaged over the folds of cross validation are plotted as a function of the number of relevant SNPs randomly excluded (left) and number of irrelevant SNPs randomly included (right) in the RRM.
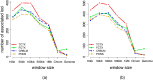
 and squared error are computed using the LMM and averaged over the folds. The plots show the averaged log likelihood (blue) and squared error (purple) as a function of k.
and squared error are computed using the LMM and averaged over the folds. The plots show the averaged log likelihood (blue) and squared error (purple) as a function of k.
References
-
- Goddard M. E., Wray N. R., Verbyla K. & Visscher P. M. Estimating Effects and Making Predictions from Genome-Wide Marker Data. Statistical Science 24, 517–529 (2009).
-
- Yu J., Pressoir G., Briggs W. H., Vroh Bi I., Yamasaki M., Doebley J. F., McMullen M. D., Gaut B. S., Nielsen D. M. & Holland J. B. et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nature Genetics 38, 203–208 (2006). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

