Unravelling daily human mobility motifs
- PMID: 23658117
- PMCID: PMC3673164
- DOI: 10.1098/rsif.2013.0246
Unravelling daily human mobility motifs
Abstract
Human mobility is differentiated by time scales. While the mechanism for long time scales has been studied, the underlying mechanism on the daily scale is still unrevealed. Here, we uncover the mechanism responsible for the daily mobility patterns by analysing the temporal and spatial trajectories of thousands of persons as individual networks. Using the concept of motifs from network theory, we find only 17 unique networks are present in daily mobility and they follow simple rules. These networks, called here motifs, are sufficient to capture up to 90 per cent of the population in surveys and mobile phone datasets for different countries. Each individual exhibits a characteristic motif, which seems to be stable over several months. Consequently, daily human mobility can be reproduced by an analytically tractable framework for Markov chains by modelling periods of high-frequency trips followed by periods of lower activity as the key ingredient.
Keywords: human dynamics; mobile phone; motifs; networks.
Figures
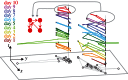
 . By contrast, the daily average number of nodes is
. By contrast, the daily average number of nodes is  , and the average number of edges is
, and the average number of edges is  . The left user prefers commuting to one place and visits the other locations during a single tour, whereas the right user prefers to visit the daily locations during a single tour. On the last day, both users visit not only four locations, but also share the same daily profile consisting of two tours with one and two destinations, respectively.
. The left user prefers commuting to one place and visits the other locations during a single tour, whereas the right user prefers to visit the daily locations during a single tour. On the last day, both users visit not only four locations, but also share the same daily profile consisting of two tours with one and two destinations, respectively.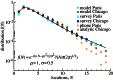
 with μ = 1 and σ = 0.5. The distributions extracted from activity and travel surveys as well as from mobile phone billing data show similar behaviour. Moreover, the distributions of our perturbation model (see §3 and figure 6 for details) generated both analytically and numerically have the same shape. The broad distribution shows that although most of the people visit less than five locations, a small fraction behave significantly differently because people report visits up to 17 different places within a day in our surveys. Note that due to the mobile phone data limitations, the tail of the corresponding distribution is below the other datasets.
with μ = 1 and σ = 0.5. The distributions extracted from activity and travel surveys as well as from mobile phone billing data show similar behaviour. Moreover, the distributions of our perturbation model (see §3 and figure 6 for details) generated both analytically and numerically have the same shape. The broad distribution shows that although most of the people visit less than five locations, a small fraction behave significantly differently because people report visits up to 17 different places within a day in our surveys. Note that due to the mobile phone data limitations, the tail of the corresponding distribution is below the other datasets.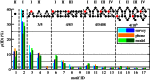

References
-
- Anderson RM, May RM. 1992. Infectious diseases in humans. Oxford, UK: Oxford University Press
-
- Lloyd AL, May RM. 2001. How viruses spread among computers and people. Science 292, 1316–131710.1126/science.1061076 (doi:10.1126/science.1061076) - DOI - DOI - PubMed
-
- Hufnagel L, Brockmann D, Geisel T. 1992. Forecast and control of epidemics in a globalized world. Proc. Natl Acad. Sci. USA 101, 15124–1512910.1073/pnas.0308344101 (doi:10.1073/pnas.0308344101) - DOI - DOI - PMC - PubMed
-
- Colizza V, Pastor-Satorras R, Vespignani A. 2007. Reaction–diffusion processes and metapopulation models in heterogeneous networks. Nat. Phys. 3, 276–28210.1038/nphys560 (doi:10.1038/nphys560) - DOI - DOI
-
- Balcan D, Colizza V, Goncalves B, Hu H, Ramasco JJ, Vespignani A. 2009. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl Acad. Sci. USA 106, 21 484–21 48910.1073/pnas.0906910106 (doi:10.1073/pnas.0906910106) - DOI - DOI - PMC - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
