Humans exploit the biomechanics of bipedal gait during visually guided walking over complex terrain
- PMID: 23658204
- PMCID: PMC3673057
- DOI: 10.1098/rspb.2013.0700
Humans exploit the biomechanics of bipedal gait during visually guided walking over complex terrain
Abstract
How do humans achieve such remarkable energetic efficiency when walking over complex terrain such as a rocky trail? Recent research in biomechanics suggests that the efficiency of human walking over flat, obstacle-free terrain derives from the ability to exploit the physical dynamics of our bodies. In this study, we investigated whether this principle also applies to visually guided walking over complex terrain. We found that when humans can see the immediate foreground as little as two step lengths ahead, they are able to choose footholds that allow them to exploit their biomechanical structure as efficiently as they can with unlimited visual information. We conclude that when humans walk over complex terrain, they use visual information from two step lengths ahead to choose footholds that allow them to approximate the energetic efficiency of walking in flat, obstacle-free environments.
Keywords: dynamic walking; human locomotion; inverted pendulum; visual control.
Figures





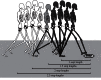
References
-
- Hodgins J, Raibert M. 1990. Biped gymnastics. Int. J. Robot. Res. 9, 115–12810.1177/027836499000900209 (doi:10.1177/027836499000900209) - DOI - DOI
-
- Kuo A. 2007. The six determinants of gait and the inverted pendulum analogy: a dynamic walking perspective. Hum. Mov. Sci. 26, 617–65610.1016/j.humov.2007.04.003 (doi:10.1016/j.humov.2007.04.003) - DOI - DOI - PubMed
-
- Kuo A, Donelan J. 2010. Dynamic principles of gait and their clinical implications. Phys. Ther. 90, 157–17410.2522/ptj.20090125 (doi:10.2522/ptj.20090125) - DOI - DOI - PMC - PubMed
-
- Kuo A. 1999. Stabilization of lateral motion in passive dynamic walking. Int. J. Robot. Res. 18, 917–93010.1177/02783649922066655 (doi:10.1177/02783649922066655) - DOI - DOI
-
- McGeer T. 1990. Passive dynamic walking. Int. J. Robot. Res. 9, 62–8210.1177/027836499000900206 (doi:10.1177/027836499000900206) - DOI - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

