Analysis of the stabilized supralinear network

Abstract

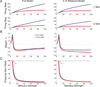
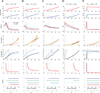
We study a rate-model neural network composed of excitatory and inhibitory neurons in which neuronal input-output functions are power laws with a power greater than 1, as observed in primary visual cortex. This supralinear input-output function leads to supralinear summation of network responses to multiple inputs for weak inputs. We show that for stronger inputs, which would drive the excitatory subnetwork to instability, the network will dynamically stabilize provided feedback inhibition is sufficiently strong. For a wide range of network and stimulus parameters, this dynamic stabilization yields a transition from supralinear to sublinear summation of network responses to multiple inputs. We compare this to the dynamic stabilization in the balanced network, which yields only linear behavior. We more exhaustively analyze the two-dimensional case of one excitatory and one inhibitory population. We show that in this case, dynamic stabilization will occur whenever the determinant of the weight matrix is positive and the inhibitory time constant is sufficiently small, and analyze the conditions for supersaturation, or decrease of firing rates with increasing stimulus contrast (which represents increasing input firing rates). In work to be presented elsewhere, we have found that this transition from supralinear to sublinear summation can explain a wide variety of nonlinearities in cerebral cortical processing.

Figure 1. Two neuron approximation of the full ring model

(A) The reduced version of the model (right) produces qualitatively similar curves of response vs. stimulus strength c as the full model (left; for the full model, this is the response of the cells at θ = 0°). The top plots show the response curves for a stimulus composed of a single grating with orientation θ = 0° and the bottom plots show the response for a two-grating stimulus composed of the grating at θ = 0° and a grating at θ = 90°. In the 2-D reduced model, these two cases are represented by using Ψ = 0.774 for one grating and Ψ = 1.024 for two gratings (see Eq. (21) for the definition of Ψ and the text after Eq. (25) for the method we used to calculate these values). (B) Full and reduced models show a similar stimulus-strength-dependent transition from supralinear summation (weight > 1) to sublinear summation (weight < 1) of the responses to two gratings, where the weight w is defined as follows. For the full model, for either E or I cells, we let R₁(θ), R₂(θ), and R₁₂(θ) be the response to one grating, the other grating, or the superposition of the two, and we define $w=\frac{R_{12}(0)}{R_1(0)+R_2(0)}$, where θ = 0 is the orientation of the first grating. For the reduced model, we define the weight as $w=\frac{R_{12}}{R_1+R_2}$, where R₁, and R₁₂ are the responses to one or two gratings (modeled by the two values of Ψ given above) and we set R₂ = 0 (by the way we defined the reduction, R₁, R₂ and R₁₂ should approximate the responses of the full model at θ = 0). (C) Full and reduced models have nearly identical stimulus-strength-dependent tuning for the width in orientation, σ_stim, of a feedforward stimulus (full model: width of Gaussian stimulus centered at θ = 0 with given stimulus strength c that gives the strongest response in cells at θ = 0; reduced model: Ψ is computed for each stimulus width as described in the text after Eq. (25), and plot shows width whose Ψ gives maximal response). In all curves, red shows E cells and blue shows I cells. All responses are steady-state responses. Full model solutions found by simulating until convergence to steady state. Parameters: J_EE = 2.5, J_IE = 2.4, J_EI = 1.3, J_II = 1.0, τ_E = 20 ms, τ_I = 10 ms, k = 0.04, n = 2.0, σ_ori = 32°; σ_stim = 30° in A,B.

Figure 2. Behavior of the 2D Model in Different Parameter Regimes

Each column corresponds to a different connectivity matrix J, corresponding to different conditions on Ω_E and Ω_I as indicated at top. In all cases, Det J > 0, n = 2.0, k = 0.04, and g_E = g_I = 1. The first column uses the same parameters as the 2-D reduced model in Fig. 1. In all figures the horizontal axis is stimulus strength c; Fig. 3 shows all plots (and one additional set of plots) for the smaller range c ∈ [0, 40]. Top row: E (red, top) and I (blue, bottom) firing rates, r_E and r_I, at fixed point. For cases with Ω_E < 0, dashed vertical lines indicate analytic calculations for c at which r_E goes to zero (Sec. 5.2.2) and, for Ω_E < Ω_I, at which r_E peaks (Eq. 41). Second Row: Weights reecting supralinear (weight > 1) or sublinear (weight < 1) summation in an equivalent ring model, computed as in Fig. 1B. Red and blue indicate E- and I-subnetworks, respectively. Inset in column E shows supralinear responses at low values of c. Third Row: Iterative solutions for r_E in the high-contrast regime (Eq. 43). We plot r_E[t] = y_E[t]c/(ψ‖J‖) vs. c, for t = 1, 5, 10, 14, 19 iterations (blue to cyan curves); black curves are exact solutions. Iterative solutions are shown only over the range for which they are real. (Iterative solutions in the low-contrast regime are shown in Fig. 3.) Fourth Row: Values of q = τ_I/τ_E separating regions in which fixed point is stable (below red line) vs. unstable (above red line). Fifth Row: Horizontal lines showing the extent of the sublinear regime according to the different definitions introduced in Sec. 5.4. Blue and red lines (E component solid, I component dashed): definitions 1 (normalization in corresponding high-dimensional ring model) and 5 (r a sublinear function of c), respectively. Green line: definition 2 (excitatory subnetwork unstable). The cyan lines show the range where the modulus of each eigenvalue of the Jacobian is > 1; sublinear regime according to definition 3 (instability of low-contrast iterative solution) or 4 (stability of high-contrast iterative solution) is the region in which either (def. 3) or both (def. 4) lines are present. Parameters used: ψ = 0.774 or, for two-grating case in 2nd row, ψ = 1.024 (the values of Ψ in Fig. 1); J_EI = 1.3; J_EE = 2.5, except 0.8 in (D); J_II = 1.0, except 2.2 in (C) and 5.0 in (D); J_IE = 2.4, 4.7, 4.7, 3.6, 2.2 in (A) to (E), respectively.

Figure 3. Crossover of the 2D Model to the High Contrast Sublinear Regime for Different Network Parameters

The plots in this figure are the same as the ones in Fig. 2, except that (1) only the range of stimulus strengths, c, from 0 to 40 is shown, to highlight the transition to the sublinear regime as c grows and (2) we also illustrate the low-contrast iterative solutions for r_E, which have been inserted as the third row (conventions as for high-contrast iterative solutions, except here red to yellow curves represent 1 to 19 iterations). See the caption of Fig. 2 for explanation of plots and parameters. The extra horizontal axes at the bottom translate the stimulus strengths into values of α as defined in Eq. (5). In addition, vertical dashed lines in the first to fifth rows indicate the transition points to the sublinear regime, according to the different definitions introduced in Sec. 5.4 and illustrated in the bottom row, with definitions 1 to 5 corresponding to colors blue, green, orange, cyan and red, respectively (for definitions 1 and 5 the line is drawn at the point where the condition holds for both E and I components). The values of the α’s at these transition lines, in the order mentioned, are (1.4, 0.7, 1.4, 1.4, 2.4), (1.0, 1.4, 1.4, 1.4, 16.3), (2.4, 1.1, 3.1, 3.1, −), (0.2, 4.7, 1.0, 28.5, −), and (0.8, 0.6, 0.8, 0.8, 0.8) in columns A to E, respectively. Notice that the transitions to the sublinear regime typically happen for α ~ 1, as expected.

Figure 4. Behavior of the Full Ring Model in Different Parameter Regimes

Behavior of the steady state of the ring network of Sec. 4.1, in the same parameter regimes as in Fig. 2. The ring network’s connectivity matrix is given by Eq. (25), with different J’s in different columns equal to those in the corresponding column of Fig. 2. The rest of the parameters are the same as in the left column of Fig. 1 (in particular, all parameters of column A match those of Fig. 1, left column). The signs and orderings of Ω_E and Ω_I are indicated on the top of each column. In all figures the horizontal axis is stimulus strength c. Top row: E (red) and I (blue) firing rates, r_E(θ = 0) and r_I (θ = 0), at fixed point. For cases with Ω_E < 0, dashed vertical lines indicate analytic calculations for c in the 2-D reduced model at which r_E goes to zero (Section 5.2.2) and, for Ω_E < Ω_I, at which r_E peaks (Eq. 41). Second Row: Weights reecting supralinear summation (weight > 1) or sublinear summation (weight < 1) computed as in Fig. 1B. Again, red and blue indicate E-and I-subnetworks, respectively. Inset in column E shows supralinear responses at low values of c. Third Row: The red and blue curves show Ψ_E ≡ w⃗ · r̂_E and Ψ_I ≡ w⃗ · r̂_I, which we approximated by ψ = w⃗ · ĝ^․n (green lines) in the 2-D reduction for the case of a one-grating stimulus (see the discussion at the end of Sec. 5.3). Fourth Row: The same as the third row, but for two-grating stimuli. Fifth Row: The red, blue and green curves show the ratios of the red, blue and green curves in the fourth row (two gratings) to those in the third row (one grating), respectively.