Capillarity-induced ordering of spherical colloids on an interface with anisotropic curvature
- PMID: 23690591
- PMCID: PMC3677486
- DOI: 10.1073/pnas.1222196110
Capillarity-induced ordering of spherical colloids on an interface with anisotropic curvature
Abstract
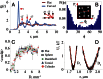
Objects floating at a liquid interface, such as breakfast cereals floating in a bowl of milk or bubbles at the surface of a soft drink, clump together as a result of capillary attraction. This attraction arises from deformation of the liquid interface due to gravitational forces; these deformations cause excess surface area that can be reduced if the particles move closer together. For micrometer-sized colloids, however, the gravitational force is too small to produce significant interfacial deformations, so capillary forces between spherical colloids at a flat interface are negligible. Here, we show that this is different when the confining liquid interface has a finite curvature that is also anisotropic. In that case, the condition of constant contact angle along the three-phase contact line can only be satisfied when the interface is deformed. We present experiments and numerical calculations that demonstrate how this leads to quadrupolar capillary interactions between the particles, giving rise to organization into regular square lattices. We demonstrate that the strength of the governing anisotropic interactions can be rescaled with the deviatoric curvature alone, irrespective of the exact shape of the liquid interface. Our results suggest that anisotropic interactions can easily be induced between isotropic colloids through tailoring of the interfacial curvature.
Keywords: Young-Laplace equation; colloidal interactions; pickering; self-assembly.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

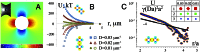

References
-
- Li F, Josephson DP, Stein A. Colloidal assembly: The road from particles to colloidal molecules and crystals. Angew Chem Int Ed Engl. 2011;50(2):360–388. - PubMed
-
- Vanmaekelbergh D. Self-assembly of colloidal nanocrystals as route to novel classes of nanostructured materials. Nano Today. 2011;6(4):419–437.
-
- Zhang J, Li Y, Zhang X, Yang B. Colloidal self-assembly meets nanofabrication: From two-dimensional colloidal crystals to nanostructure arrays. Adv Mater (Deerfield Beach Fla) 2010;22(38):4249–4269. - PubMed
-
- Wang Y, et al. Colloids with valence and specific directional bonding. Nature. 2012;491(7422):51–55. - PubMed
-
- Mao X, Chen Q, Granick S. Entropy favours open colloidal lattices. Nat Mater. 2013;12(3):217–222. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

