Procedures for numerical analysis of circadian rhythms
- PMID: 23710111
- PMCID: PMC3663600
- DOI: 10.1080/09291010600903692
Procedures for numerical analysis of circadian rhythms
Abstract
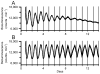
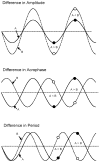
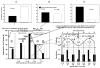
This article reviews various procedures used in the analysis of circadian rhythms at the populational, organismal, cellular and molecular levels. The procedures range from visual inspection of time plots and actograms to several mathematical methods of time series analysis. Computational steps are described in some detail, and additional bibliographic resources and computer programs are listed.
Keywords: Biostatistics; chronobiology; chronomics; circadian rhythm; time series analysis.
Figures








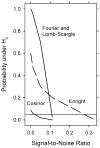
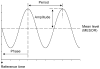


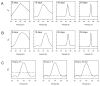




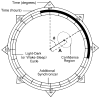


Similar articles
-
'Chronomics' in ICU: circadian aspects of immune response and therapeutic perspectives in the critically ill.Intensive Care Med Exp. 2014 Dec;2(1):18. doi: 10.1186/2197-425X-2-18. Epub 2014 May 14. Intensive Care Med Exp. 2014. PMID: 26266918 Free PMC article.
-
Bibliometric and visual analysis of circadian rhythms in depression from 2004 to 2024.Ann Gen Psychiatry. 2025 May 14;24(1):27. doi: 10.1186/s12991-025-00565-x. Ann Gen Psychiatry. 2025. PMID: 40369622 Free PMC article.
-
Circadian rhythmicity of body temperature and metabolism.Temperature (Austin). 2020 Apr 17;7(4):321-362. doi: 10.1080/23328940.2020.1743605. eCollection 2020. Temperature (Austin). 2020. PMID: 33251281 Free PMC article. Review.
-
Ethical and methodological standards for laboratory and medical biological rhythm research.Chronobiol Int. 2008 Nov;25(6):999-1016. doi: 10.1080/07420520802544530. Chronobiol Int. 2008. PMID: 19005901
-
Postoperative circadian disturbances.Dan Med Bull. 2010 Dec;57(12):B4205. Dan Med Bull. 2010. PMID: 21122464 Review.
Cited by
-
Photoperiodic influences on ultradian rhythms of male Siberian hamsters.PLoS One. 2012;7(7):e41723. doi: 10.1371/journal.pone.0041723. Epub 2012 Jul 27. PLoS One. 2012. PMID: 22848579 Free PMC article.
-
Desoxycorticosterone pivalate-salt treatment leads to non-dipping hypertension in Per1 knockout mice.Acta Physiol (Oxf). 2017 May;220(1):72-82. doi: 10.1111/apha.12804. Epub 2016 Oct 3. Acta Physiol (Oxf). 2017. PMID: 27636900 Free PMC article.
-
Seizure-related differences in biosignal 24-h modulation patterns.Sci Rep. 2022 Sep 5;12(1):15070. doi: 10.1038/s41598-022-18271-z. Sci Rep. 2022. PMID: 36064877 Free PMC article.
-
Seasonal patterns of body temperature in response to experimental photoperiod variation in a non-hibernating ground squirrel.J Comp Physiol B. 2023 Mar;193(2):219-226. doi: 10.1007/s00360-023-01477-6. Epub 2023 Feb 25. J Comp Physiol B. 2023. PMID: 36840751
-
Daily rhythms of rectal and body surface temperatures in donkeys during the cold-dry (harmattan) and hot-dry seasons in a tropical savannah.Int J Biometeorol. 2018 Dec;62(12):2231-2243. doi: 10.1007/s00484-018-1626-z. Epub 2018 Oct 29. Int J Biometeorol. 2018. PMID: 30374600
References
-
- Akiyama T. Entrainment of the circatidal swimming activity rhythm in the cumacean Dimorphostylis asiatica (Crustacea) to 12.5-hour hydrostatic pressure cycles. Zool Sci. 2004;21:29–38. - PubMed
-
- Albers HE, Gerall AA, Axelson JF. Effect of reproductive state on circadian periodicity in the rat. Physiol Behav. 1981;26:21–25. - PubMed
-
- Albert PS. On analyzing circadian rhythms data using nonlinear mixed models with harmonic terms. Biometrics. 2005;61:1115–1120. - PubMed
-
- Almirall H. Modeling the body temperature throughout the day with a two-term function. Behav Res Methods Instrum Comput. 1997;29:595–599.
-
- Alonso I, Fernández JR. Nonlinear estimation and statistical testing of periods in nonsinusoidal longitudinal time series with unequidistant observations. Chronobiol Int. 2001;18:285–308. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
