Metabolic scaling in solid tumours
- PMID: 23727729
- PMCID: PMC3670262
- DOI: 10.1038/srep01938
Metabolic scaling in solid tumours
Abstract
Tumour metabolism is an outstanding topic of cancer research, as it determines the growth rate and the global activity of tumours. Recently, by combining the diffusion of oxygen, nutrients, and metabolites in the extracellular environment, and the internal motions that mix live and dead cells, we derived a growth law of solid tumours which is linked to parameters at the cellular level. Here we use this growth law to obtain a metabolic scaling law for solid tumours, which is obeyed by tumours of different histotypes both in vitro and in vivo, and we display its relation with the fractal dimension of the distribution of live cells in the tumour mass. The scaling behaviour is related to measurable parameters, with potential applications in the clinical practice.
Figures

 from Eq. (5), while the dashed line is
from Eq. (5), while the dashed line is  from Eq. (6). The volume range corresponds to a minimum radius of 5 μm (i.e., approximately a single cell), up to a maximum of 2000 μm. The arrow marks the volume corresponding to a nearly spherical avascular tumour with a diameter of 1 mm.
from Eq. (6). The volume range corresponds to a minimum radius of 5 μm (i.e., approximately a single cell), up to a maximum of 2000 μm. The arrow marks the volume corresponding to a nearly spherical avascular tumour with a diameter of 1 mm.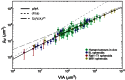
 , Eq. (5), at small tumour size, while the dashed line is the approximation
, Eq. (5), at small tumour size, while the dashed line is the approximation  , Eq. (6), at large tumour size. Data from human tumours (green circles) include breast, uterine and ovarian carcinomas, melanomas, thyroid carcinomas, colon and lung carcinomas.
, Eq. (6), at large tumour size. Data from human tumours (green circles) include breast, uterine and ovarian carcinomas, melanomas, thyroid carcinomas, colon and lung carcinomas.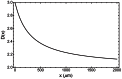


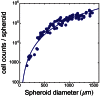
 and
and  .
.
 and
and  .
.
References
-
- Helmlinger G., Yuan F., Dellan M. & Jain R. K. Interstitial pH and pO2 gradients in solid tumors in vivo: high resolution measurements reveal al lack of correlation. Nat. Med. 3, 177–182 (1997). - PubMed
-
- Li C. K. N. The glucose distribution in 9L rat brain multicell tumour spheroids and its effect on cell necrosis. Cancer 50, 2066–2073 (1982). - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

