Patient-Specific Models of Cardiac Biomechanics
- PMID: 23729839
- PMCID: PMC3667962
- DOI: 10.1016/j.jcp.2012.09.015
Patient-Specific Models of Cardiac Biomechanics
Abstract
Patient-specific models of cardiac function have the potential to improve diagnosis and management of heart disease by integrating medical images with heterogeneous clinical measurements subject to constraints imposed by physical first principles and prior experimental knowledge. We describe new methods for creating three-dimensional patient-specific models of ventricular biomechanics in the failing heart. Three-dimensional bi-ventricular geometry is segmented from cardiac CT images at end-diastole from patients with heart failure. Human myofiber and sheet architecture is modeled using eigenvectors computed from diffusion tensor MR images from an isolated, fixed human organ-donor heart and transformed to the patient-specific geometric model using large deformation diffeomorphic mapping. Semi-automated methods were developed for optimizing the passive material properties while simultaneously computing the unloaded reference geometry of the ventricles for stress analysis. Material properties of active cardiac muscle contraction were optimized to match ventricular pressures measured by cardiac catheterization, and parameters of a lumped-parameter closed-loop model of the circulation were estimated with a circulatory adaptation algorithm making use of information derived from echocardiography. These components were then integrated to create a multi-scale model of the patient-specific heart. These methods were tested in five heart failure patients from the San Diego Veteran's Affairs Medical Center who gave informed consent. The simulation results showed good agreement with measured echocardiographic and global functional parameters such as ejection fraction and peak cavity pressures.
Keywords: Cardiac Biomechanics; Fiber Architecture; Finite Elements; Heart Failure; Patient-specific Models; Unloaded Geometry.
Figures
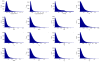



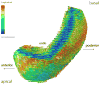



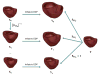

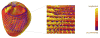







References
-
- Alastrue V, Garía A, Peña E, Rodríguez J, Martínez M, Doblaré M. Numerical framework for patient-specific computational modelling of vascular tissue. International Journal for Numerical Methods in Biomedical Engineering. 2010;26 (1):35–51.
-
- Alexander A, Hasan K, Kindlmann G, Parker D, Tsuruda J. A geometric analysis of diffusion tensor measurements of the human brain. Magnetic Resonance in Medicine. 2000;44 (2):283–291. - PubMed
-
- Alexander D, Pierpaoli C, Basser P, Gee J. Spatial transformations of diffusion tensor magnetic resonance images. Medical Imaging, IEEE Transactions on. 2001;20 (11):1131–1139. - PubMed
-
- Arsigny V, Fillard P, Pennec X, Ayache N. Fast and simple calculus on tensors in the log-euclidean framework. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2005;2005:115–122. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
