Coupled oscillations of a protein microtubule immersed in cytoplasm: an orthotropic elastic shell modeling

Abstract

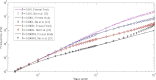
Revealing vibration characteristics of sub-cellular structural components such as membranes and microtubules has a principal role in obtaining a deeper understanding of their biological functions. Nevertheless, limitations and challenges in biological experiments at this scale necessitates the use of mathematical and computational models as an alternative solution. As one of the three major cytoskeletal filaments, microtubules are highly anisotropic structures built from tubulin heterodimers. They are hollow cylindrical shells with a ∼ 25 nm outer diameter and are tens of microns long. In this study, a mechanical model including the effects of the viscous cytosol and surrounding filaments is developed for predicting the coupled oscillations of a single microtubule immersed in cytoplasm. The first-order shear deformation shell theory for orthotropic materials is used to model the microtubule, whereas the motion of the cytosol is analyzed by considering the Stokes flow. The viscous cytosol and the microtubule are coupled through the continuity condition across the microtubule-cytosol interface. The stress and velocity fields in the cytosol induced by vibrating microtubule are analytically determined. Finally, the influences of the dynamic viscosity of the cytosol, filament network elasticity, microtubule shear modulus, and circumferential wave-number on longitudinal, radial, and torsional modes of microtubule vibration are elucidated.

Keywords: Cell mechanics; Coupled frequency; Microtubule-cytoplasm system; Orthotropic elastic shell.

Fig. 1

Configuration of typical 13-3 microtubule. Adopted from de Pable et al. [30] and Wang and Zhang [12]

Fig. 2

Mode shapes along the circumferential (torsional) and longitudinal directions

Fig. 3

The dispersion curves of the microtubule frequencies with n = 1 − 5, E_x = 1 GPa, E_θ = 1 MPa and E_xθ = 1 MPa; a torsional (circumferential) mode, b radial mode and c longitudinal mode

Fig. 4

The dispersion curves of the microtubule frequencies with E_x = 1 GPa, E_θ = 1 MPa, G_xθ = 1 MPa and ξ = 0; an = 1, bn = 3 and cn = 5; panels d through f show results obtained with the Sanders-Koiterclassical shell theory

Fig. 5

Effect of the cytosol viscosity on the torsional microtubule frequency for n = 2, E_x = 1 GPa, E_θ = 1 MPa, G_xθ = 1 MPa, ξ = 0 and four different cytosol viscosities, μ = 0, 0.001, 0.005 and 0.01

Fig. 6

The dependence of the microtubule frequency on the shear modulus with n = 1, E_x = 1 GPa, E_θ = 1 MPa, G_xθ = 1 MPa, ξ = 0 and μ = 0; a torsional mode and b longitudinal mode