Community flux balance analysis for microbial consortia at balanced growth

Abstract

A central focus in studies of microbial communities is the elucidation of the relationships between genotype, phenotype, and dynamic community structure. Here, we present a new computational method called community flux balance analysis (cFBA) to study the metabolic behavior of microbial communities. cFBA integrates the comprehensive metabolic capacities of individual microorganisms in terms of (genome-scale) stoichiometric models of metabolism, and the metabolic interactions between species in the community and abiotic processes. In addition, cFBA considers constraints deriving from reaction stoichiometry, reaction thermodynamics, and the ecosystem. cFBA predicts for communities at balanced growth the maximal community growth rate, the required rates of metabolic reactions within and between microbes and the relative species abundances. In order to predict species abundances and metabolic activities at the optimal community growth rate, a nonlinear optimization problem needs to be solved. We outline the methodology of cFBA and illustrate the approach with two examples of microbial communities. These examples illustrate two useful applications of cFBA. Firstly, cFBA can be used to study how specific biochemical limitations in reaction capacities cause different types of metabolic limitations that microbial consortia can encounter. In silico variations of those maximal capacities allow for a global view of the consortium responses to various metabolic and environmental constraints. Secondly, cFBA is very useful for comparing the performance of different metabolic cross-feeding strategies to either find one that agrees with experimental data or one that is most efficient for the community of microorganisms.

Figure 1. Metabolic network overview of a microbial community of two microorganisms engaging in metabolic cross feeding.

Species i and j exchange ammonium (NH₃) and succinate (Succ). These metabolites are allowed to overflow into the environment. Species i and j respectively take up glucose (Glu) and dinitrogen gas (N₂) supplied by the environment. Each organism operates at an intracellular metabolic steady state and contains four coarse-grained metabolic processes: catabolism, anabolism, product formation and respiration. Detailed information about the stoichiometric description of this community can be found in information S1. Three types of reaction rates occur: specific fluxes (q’s; in mol•(gram biomass) ⁻¹•h^{− 1}), environment fluxes (J’s; in mol•h^{− 1}), and specific growth rates (μ; h^{− 1}). X_i and X_j denote the biomass abundances of the two microorganisms in gram biomass.

Figure 2. Illustration of environmental and metabolic limitations at the consortium level, for the consortium depicted in Figure 1E.

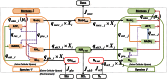
A: Optimal consortium growth rate (), in h⁻¹, as a function of fractional biomass abundance of species () at different cross-feeding (CF) reaction capacities, with all ’s in mol•h^{− 1} and all ’s in mol•g⁻¹•h^{− 1}. We consider a limited glucose (flux: and excess nitrogen (flux: and vary the flux bounds for CF fluxes (i.e. succinate () and ammonia () production fluxes) to distinguish different limitation regimes and optimality states: i. infinite CF when, ii. critical CF (), iii. two cases for above critical CF: curve I (for: and curve II (for: , and iv. below critical CF (for: . This figure indicates that the CF reactions determine the optimal value of the community growth rate and the optimal fractional biomass abundance. B: A contour plot is generated for the optimal community growth rate as function of the upper bound of the succinate production flux by species and the ammonia production flux of species . The environmental conditions are the same as in Figure 2A. The different points depict the various cross-feeding regimes distinguished in Figure 2A (• Above Critical CF – I, ★ Above Critical CF – II, ♦Below Critical CF). This figure indicates that the CF fluxes between the organisms determine the optimal community state at a fixed environment. C: Contour plot of the maximum community growth rate, as a function of the environment while cross-feeding capacities are kept unconstrained. This figure indicates that the optimal state of the ecosystem can be determined by specific environmental fluxes.

Figure 3. Illustration of cFBA applied to a genome-scale stoichiometric model of a microbial consortium evolved in a chemostat.

A: Consortium of two E. coli strains; one is a glucose consumer ‘’ and other is a specialist acetate consumer ‘’. They both take up glucose with specific glucose consumption fluxes and in mmol•g⁻¹•h^{− 1} but ‘’ does this with lower activity than ‘’. Strain ‘’ produces acetate with flux and strain ‘’ consumes it via flux . In the chemostat, glucose is provided at a constant rate . Andis the acetate production rate (mol•h^{− 1}). Various metabolites could be cross-fed between both organisms besides acetate, which leads to the question whether those alternative metabolites can be predicted by cFBA. B: A biomass ratio scan was performed and the community growth rate is plotted as a function of the steady-state biomass ratio. The following parameter were determined from the experimental data of Rosenzweig et al. (1994):; ; dilution rate (D) =  = 0.2; and steady state biomass ratio . To plot the ‘Below Critical Cross-feeding’ curve, cross-feeding fluxes were constrained as indicated in the plot, while for the ‘Infinite Cross-feeding” curve, unconstrained acetate cross-feeding capacities were assumed. C: Percentage change in minimum glucose uptake rate needed to achieve the growth rate of 0.2 h^{− 1} for alternative cross-feeding metabolites (one-at-a-time).

Figure 4. General structure of the stoichiometric matrix of a microbial consortium.

The community stoichiometry matrix has rows (metabolites) and columns (reactions) and is created by merging individual stoichiometric matrices ( ,) of community microorganisms and the environmental fluxes. The species-specific stoichiometric matrices have a consistent organization of metabolites (intracellular (), cross-feeding () and extracellular ()) and reactions (intracellular (), cross-feeding (), unique transport () and environmental exchange ()). Any sub-matrix notation has species name ( or ) as subscript and type of metabolites and reactions as superscript. The community stoichiometry matrix multiplied by the fractional biomass matrix and flux vector then gives the steady state mass balances of the community (equation (3)).