The effects of neural gain on attention and learning
- PMID: 23770566
- PMCID: PMC3725201
- DOI: 10.1038/nn.3428
The effects of neural gain on attention and learning
Abstract
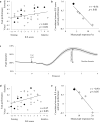
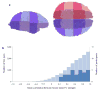
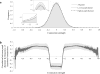
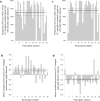
Attention is commonly thought to be manifest through local variations in neural gain. However, what would be the effects of brain-wide changes in gain? We hypothesized that global fluctuations in gain modulate the breadth of attention and the degree to which processing is focused on aspects of the environment to which one is predisposed to attend. We found that measures of pupil diameter, which are thought to track levels of locus coeruleus norepinephrine activity and neural gain, were correlated with the degree to which learning was focused on stimulus dimensions that individual human participants were more predisposed to process. In support of our interpretation of this effect in terms of global changes in gain, we found that the measured pupillary and behavioral variables were strongly correlated with global changes in the strength and clustering of functional connectivity, as brain-wide fluctuations of gain would predict.
Figures



Comment in
-
Brain-wide gain modulation: the rich get richer.Nat Neurosci. 2013 Aug;16(8):989-90. doi: 10.1038/nn.3471. Nat Neurosci. 2013. PMID: 23887133 No abstract available.
Similar articles
-
Brain-wide gain modulation: the rich get richer.Nat Neurosci. 2013 Aug;16(8):989-90. doi: 10.1038/nn.3471. Nat Neurosci. 2013. PMID: 23887133 No abstract available.
-
Pupil size signals mental effort deployed during multiple object tracking and predicts brain activity in the dorsal attention network and the locus coeruleus.J Vis. 2014 Apr 1;14(4):1. doi: 10.1167/14.4.1. J Vis. 2014. PMID: 24692319
-
Pupil tracks statistical regularities: behavioral and neural implications.J Integr Neurosci. 2020 Dec 30;19(4):729-731. doi: 10.31083/j.jin.2020.04.331. J Integr Neurosci. 2020. PMID: 33378847
-
Fluid intelligence and the locus coeruleus-norepinephrine system.Proc Natl Acad Sci U S A. 2021 Nov 16;118(46):e2110630118. doi: 10.1073/pnas.2110630118. Proc Natl Acad Sci U S A. 2021. PMID: 34764223 Free PMC article. Review.
-
Role of locus coeruleus in attention and behavioral flexibility.Biol Psychiatry. 1999 Nov 1;46(9):1309-20. doi: 10.1016/s0006-3223(99)00140-7. Biol Psychiatry. 1999. PMID: 10560036 Review.
Cited by
-
Plasticity of cortical excitatory-inhibitory balance.Annu Rev Neurosci. 2015 Jul 8;38:195-219. doi: 10.1146/annurev-neuro-071714-034002. Epub 2015 Apr 9. Annu Rev Neurosci. 2015. PMID: 25897875 Free PMC article. Review.
-
Target detection increases pupil diameter and enhances memory for background scenes during multi-tasking.Sci Rep. 2019 Mar 27;9(1):5255. doi: 10.1038/s41598-019-41658-4. Sci Rep. 2019. PMID: 30918293 Free PMC article.
-
Pupil-linked arousal modulates behavior in rats performing a whisker deflection direction discrimination task.J Neurophysiol. 2018 Oct 1;120(4):1655-1670. doi: 10.1152/jn.00290.2018. Epub 2018 Jul 11. J Neurophysiol. 2018. PMID: 29995602 Free PMC article.
-
Circuit mechanisms for the chemical modulation of cortex-wide network interactions and behavioral variability.Sci Adv. 2021 Jul 16;7(29):eabf5620. doi: 10.1126/sciadv.abf5620. Print 2021 Jul. Sci Adv. 2021. PMID: 34272245 Free PMC article.
-
Dynamic modulation of decision biases by brainstem arousal systems.Elife. 2017 Apr 11;6:e23232. doi: 10.7554/eLife.23232. Elife. 2017. PMID: 28383284 Free PMC article.
References
-
- Felder RM, Silverman LK. Learning and teaching styles in engineering education. J Eng Educ. 1988;78:674–681.
-
- Coffield F, Moseley D, Hall E, Ecclestone K. Learning Styles and Pedagogy in Post-16 Learning: A Systematic and Critical Review. Learning and Skills Research Centre; London: 2004.
-
- Felder RM, Spurlin J. Application, Reliability and Validity of the Index of Learning Styles. Education. 2005;21:103–112.
-
- Servan-Schreiber D, Printz H, Cohen JD. A network model of catecholamine effects: gain, signal-to-noise ratio, and behavior. Science. 1990;249:892–895. - PubMed
-
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu Rev Neurosci. 2005;28:403–450. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

