Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Dec;36(6):699-719.
doi: 10.3102/1076998610396889.

Solutions for Determining the Significance Region Using the Johnson-Neyman Type Procedure in Generalized Linear (Mixed) Models

Ann A Lazar  1 , Gary O Zerbe
Affiliations

Solutions for Determining the Significance Region Using the Johnson-Neyman Type Procedure in Generalized Linear (Mixed) Models

Ann A Lazar et al. J Educ Behav Stat. 2011 Dec.

Abstract

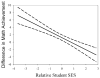
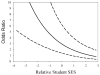
Researchers often compare the relationship between an outcome and covariate for two or more groups by evaluating whether the fitted regression curves differ significantly. When they do, researchers need to determine the "significance region," or the values of the covariate where the curves significantly differ. In analysis of covariance (ANCOVA), the Johnson-Neyman procedure can be used to determine the significance region; for the hierarchical linear model (HLM), the Miyazaki and Maier (M-M) procedure has been suggested. However, neither procedure can assume nonnormally distributed data. Furthermore, the M-M procedure produces biased (downward) results because it uses the Wald test, does not control the inflated Type I error rate due to multiple testing, and requires implementing multiple software packages to determine the significance region. In this article, we address these limitations by proposing solutions for determining the significance region suitable for generalized linear (mixed) model (GLM or GLMM). These proposed solutions incorporate test statistics that resolve the biased results, control the Type I error rate using Scheffé's method, and uses a single statistical software package to determine the significance region.

Keywords: generalized estimating equations; hierarchical linear models; longitudinal analysis; multiple testing; simultaneous testing.

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
The estimated difference (Catholic minus Public high schools) in mathematic (Math) achievement as a function of relative student SES. Differences above 0 indicate Catholic sector better, otherwise public schools. Broken lines represent 95% confidence band using Scheffé’s method.
FIGURE 2
FIGURE 2
The estimated odds ratio (solid line) of high mathematics achievement for the Catholic sector compared to public school 1296 as a function of relative student SES. Odds ratio above 1 indicates (the odds of) higher mathematics achievement score in Catholic schools compared with public school 1296, otherwise public. Broken lines represent the 95% confidence band using Scheffé’s method.
See this image and copyright information in PMC

References

    1. Coleman J, Hoffer T, Kilgore S. High school achievement: Public, Catholic, and other schools compared. New York, NY: Basic Books; 1982.
    1. Dempster AP, Rubin DB, Tsutakawa RK. Estimation in covariance components model. Journal of the American Statistical Association. 1981;76:341–353.
    1. Hunka S. Identifying regions of significance in ANCOVA problems having non-homogeneous regressions. British Journal of Mathematical and Statistical Psychology. 1995;48:161–188.
    1. Hunka S, Leighton J. Defining Johnson-Neyman regions of significance in the three-covariate ANCOVA using Mathematica. Journal of Education and Behavioral Statistics. 1997;22:361–387.
    1. Johnson PO, Fay LC. The Johnson-Neyman technique, its theory and application. Psychometrika. 1950;15:349–367. - PubMed

LinkOut - more resources