Enhancement of vibronic and ground-state vibrational coherences in 2D spectra of photosynthetic complexes
- PMID: 23778355
- PMCID: PMC3693153
- DOI: 10.1038/srep02029
Enhancement of vibronic and ground-state vibrational coherences in 2D spectra of photosynthetic complexes
Abstract
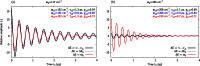
A vibronic-exciton model is applied to investigate the recently proposed mechanism of enhancement of coherent oscillations due to mixing of electronic and nuclear degrees of freedom. We study a dimer system to elucidate the role of resonance coupling, site energies, vibrational frequency and energy disorder in the enhancement of vibronic-exciton and ground-state vibrational coherences, and to identify regimes where this enhancement is significant. For a heterodimer representing two coupled bachteriochloropylls of the FMO complex, long-lived vibronic coherences are found to be generated only when the frequency of the mode is in the vicinity of the electronic energy difference. Although the vibronic-exciton coherences exhibit a larger initial amplitude compared to the ground-state vibrational coherences, we conclude that, due to the dephasing of the former, both type of coherences have a similar magnitude at longer population time.
Figures
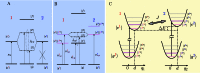
 (diamond). Signals denoted by circle symbols refer to the electronic excited-state manifold and do not involve any (purely) vibrational level whereas signals on the electronic ground-state manifold, denoted by diamonds, do (for ν ≥ 1). The diads in (B) represent the eigenstates |α〉, |β〉 involved in each signal contribution. The red contours highlight the signals for which we present detailed results below.
(diamond). Signals denoted by circle symbols refer to the electronic excited-state manifold and do not involve any (purely) vibrational level whereas signals on the electronic ground-state manifold, denoted by diamonds, do (for ν ≥ 1). The diads in (B) represent the eigenstates |α〉, |β〉 involved in each signal contribution. The red contours highlight the signals for which we present detailed results below.
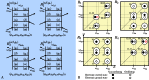
 ) is highlighted with colored areas. A significant enhancement of the dipole moment pre-factor can be observed for coherence involving eigenstates 1 and 2, which is strongly vibrational for ΔE > 99 cm−1.
) is highlighted with colored areas. A significant enhancement of the dipole moment pre-factor can be observed for coherence involving eigenstates 1 and 2, which is strongly vibrational for ΔE > 99 cm−1.

References
-
- Engel G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782 (2007). - PubMed
-
- Prokhorenko V. I., Holzwarth A. R., Nowak F. R. & Aartsma T. J. Growing-In of Optical Coherence in the FMO antenna complexes. J. Phys. Chem. B 106, 9923–9933 (2002).
-
- Savikhin S., Buck D. R. & Struve W. S. Oscillating anisotropies in a bacteriochlorophyll protein: Evidence for quantum beating between exciton levels. J. Chem. Phys. 223, 303–312 (1997).
-
- Lee H., Cheng Y.-C. & Fleming G. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 316, 1462–1465 (2007). - PubMed
-
- Caram J. R., Lewis N. H. C., Fidler A. F. & Engel G. S. Signatures of correlated excitonic dynamics in two-dimensional spectroscopy of the fenna-matthew-olson photosynthetic complex. J. Chem. Phys. 136, 104505 (2012). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

