Haplotype assembly in polyploid genomes and identical by descent shared tracts
- PMID: 23813004
- PMCID: PMC3694639
- DOI: 10.1093/bioinformatics/btt213
Haplotype assembly in polyploid genomes and identical by descent shared tracts
Abstract
Motivation: Genome-wide haplotype reconstruction from sequence data, or haplotype assembly, is at the center of major challenges in molecular biology and life sciences. For complex eukaryotic organisms like humans, the genome is vast and the population samples are growing so rapidly that algorithms processing high-throughput sequencing data must scale favorably in terms of both accuracy and computational efficiency. Furthermore, current models and methodologies for haplotype assembly (i) do not consider individuals sharing haplotypes jointly, which reduces the size and accuracy of assembled haplotypes, and (ii) are unable to model genomes having more than two sets of homologous chromosomes (polyploidy). Polyploid organisms are increasingly becoming the target of many research groups interested in the genomics of disease, phylogenetics, botany and evolution but there is an absence of theory and methods for polyploid haplotype reconstruction.
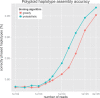
Results: In this work, we present a number of results, extensions and generalizations of compass graphs and our HapCompass framework. We prove the theoretical complexity of two haplotype assembly optimizations, thereby motivating the use of heuristics. Furthermore, we present graph theory-based algorithms for the problem of haplotype assembly using our previously developed HapCompass framework for (i) novel implementations of haplotype assembly optimizations (minimum error correction), (ii) assembly of a pair of individuals sharing a haplotype tract identical by descent and (iii) assembly of polyploid genomes. We evaluate our methods on 1000 Genomes Project, Pacific Biosciences and simulated sequence data.
Availability and implementation: HapCompass is available for download at http://www.brown.edu/Research/Istrail_Lab/.
Supplementary information: Supplementary data are available at Bioinformatics online.
Figures

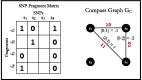
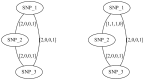
 , a non-conflicting polyploid cycle (left), and
, a non-conflicting polyploid cycle (left), and  , a conflicting polyploid cycle (right). The vector on the edge corresponds to the haplotype counts for an edge in the format [00,01,10,11]. In both compass graphs, the haplotypes are 000, 000 and 111, while the reads in
, a conflicting polyploid cycle (right). The vector on the edge corresponds to the haplotype counts for an edge in the format [00,01,10,11]. In both compass graphs, the haplotypes are 000, 000 and 111, while the reads in  are 000, 000 and 111, and the reads in
are 000, 000 and 111, and the reads in  are 00–, 01–, 10–, –00, –00, –11, 0–0, 0–0 and 1–1
are 00–, 01–, 10–, –00, –00, –11, 0–0, 0–0 and 1–1
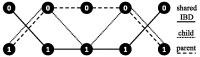
 and (bottom)
and (bottom)  corresponding to
corresponding to  and
and  , respectively
, respectively
 and (bottom)
and (bottom)  . For a k-ploid organism (in this case k = 3), a flow of k with 1 capacity on each edge corresponds to a valid assignment of haplotype paths to haplotypes of the phasing a level 1
. For a k-ploid organism (in this case k = 3), a flow of k with 1 capacity on each edge corresponds to a valid assignment of haplotype paths to haplotypes of the phasing a level 1
References
-
- Bansal V, Bafna V. HapCUT: an efficient and accurate algorithm for the haplotype assembly problem. Bioinformatics. 2008;24:i153–i159. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

