FlowMax: A Computational Tool for Maximum Likelihood Deconvolution of CFSE Time Courses
- PMID: 23826329
- PMCID: PMC3694893
- DOI: 10.1371/journal.pone.0067620
FlowMax: A Computational Tool for Maximum Likelihood Deconvolution of CFSE Time Courses
Abstract
The immune response is a concerted dynamic multi-cellular process. Upon infection, the dynamics of lymphocyte populations are an aggregate of molecular processes that determine the activation, division, and longevity of individual cells. The timing of these single-cell processes is remarkably widely distributed with some cells undergoing their third division while others undergo their first. High cell-to-cell variability and technical noise pose challenges for interpreting popular dye-dilution experiments objectively. It remains an unresolved challenge to avoid under- or over-interpretation of such data when phenotyping gene-targeted mouse models or patient samples. Here we develop and characterize a computational methodology to parameterize a cell population model in the context of noisy dye-dilution data. To enable objective interpretation of model fits, our method estimates fit sensitivity and redundancy by stochastically sampling the solution landscape, calculating parameter sensitivities, and clustering to determine the maximum-likelihood solution ranges. Our methodology accounts for both technical and biological variability by using a cell fluorescence model as an adaptor during population model fitting, resulting in improved fit accuracy without the need for ad hoc objective functions. We have incorporated our methodology into an integrated phenotyping tool, FlowMax, and used it to analyze B cells from two NFκB knockout mice with distinct phenotypes; we not only confirm previously published findings at a fraction of the expended effort and cost, but reveal a novel phenotype of nfkb1/p105/50 in limiting the proliferative capacity of B cells following B-cell receptor stimulation. In addition to complementing experimental work, FlowMax is suitable for high throughput analysis of dye dilution studies within clinical and pharmacological screens with objective and quantitative conclusions.
Conflict of interest statement
Figures

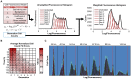
 , parameterized according to equations describing variability in staining (CV), background fluorescence (b), dye dilution (r), and a small correction for the fluorescence of the initial population of cells (s). Weights for each Gaussian correspond to cell counts in each generation. (B) Analysis of the cell fluorescence model fitting accuracy for 1,000 generated CFSE fluorescence time courses (see also Tables S3 and S4). Average percent error in generational cell counts normalized to the maximum generational cell count for each time course. Numbers indicate an error ≥ 0.5%. (C) Representative cell fluorescence model fitting to experimental data from wildtype B cells at indicated time points after start of lipopolysaccharides (LPS) stimulation (red lines indicate undivided population).
, parameterized according to equations describing variability in staining (CV), background fluorescence (b), dye dilution (r), and a small correction for the fluorescence of the initial population of cells (s). Weights for each Gaussian correspond to cell counts in each generation. (B) Analysis of the cell fluorescence model fitting accuracy for 1,000 generated CFSE fluorescence time courses (see also Tables S3 and S4). Average percent error in generational cell counts normalized to the maximum generational cell count for each time course. Numbers indicate an error ≥ 0.5%. (C) Representative cell fluorescence model fitting to experimental data from wildtype B cells at indicated time points after start of lipopolysaccharides (LPS) stimulation (red lines indicate undivided population).




Similar articles
-
Numerical modelling of label-structured cell population growth using CFSE distribution data.Theor Biol Med Model. 2007 Jul 24;4:26. doi: 10.1186/1742-4682-4-26. Theor Biol Med Model. 2007. PMID: 17650320 Free PMC article.
-
Distributed parameter identification for a label-structured cell population dynamics model using CFSE histogram time-series data.J Math Biol. 2009 Nov;59(5):581-603. doi: 10.1007/s00285-008-0244-5. Epub 2008 Dec 19. J Math Biol. 2009. PMID: 19096849
-
Deriving Quantitative Cell Biological Information from Dye-Dilution Lymphocyte Proliferation Experiments.Methods Mol Biol. 2018;1707:81-94. doi: 10.1007/978-1-4939-7474-0_6. Methods Mol Biol. 2018. PMID: 29388101 Free PMC article. Review.
-
Measuring lymphocyte proliferation, survival and differentiation using CFSE time-series data.Nat Protoc. 2007;2(9):2057-67. doi: 10.1038/nprot.2007.297. Nat Protoc. 2007. PMID: 17853861
-
Analysing cell division in vivo and in vitro using flow cytometric measurement of CFSE dye dilution.J Immunol Methods. 2000 Sep 21;243(1-2):147-54. doi: 10.1016/s0022-1759(00)00231-3. J Immunol Methods. 2000. PMID: 10986412 Review.
Cited by
-
Mechanisms of cell division as regulators of acute immune response.Syst Synth Biol. 2014 Sep;8(3):215-21. doi: 10.1007/s11693-014-9149-3. Epub 2014 Apr 29. Syst Synth Biol. 2014. PMID: 25136383 Free PMC article. Review.
-
Synergy and antagonism in the integration of BCR and CD40 signals that control B-cell proliferation.bioRxiv [Preprint]. 2024 Jul 29:2024.07.28.605521. doi: 10.1101/2024.07.28.605521. bioRxiv. 2024. Update in: Mol Syst Biol. 2025 Aug;21(8):1119-1146. doi: 10.1038/s44320-025-00124-2. PMID: 39131345 Free PMC article. Updated. Preprint.
-
Nongenetic origins of cell-to-cell variability in B lymphocyte proliferation.Proc Natl Acad Sci U S A. 2018 Mar 20;115(12):E2888-E2897. doi: 10.1073/pnas.1715639115. Epub 2018 Mar 7. Proc Natl Acad Sci U S A. 2018. PMID: 29514960 Free PMC article.
-
Marginal zone and follicular B cells respond differently to TLR4 and TLR9 stimulation.bioRxiv [Preprint]. 2025 May 25:2025.05.20.655194. doi: 10.1101/2025.05.20.655194. bioRxiv. 2025. PMID: 40475402 Free PMC article. Preprint.
-
Cyton2: A Model of Immune Cell Population Dynamics That Includes Familial Instructional Inheritance.Front Bioinform. 2021 Oct 26;1:723337. doi: 10.3389/fbinf.2021.723337. eCollection 2021. Front Bioinform. 2021. PMID: 36303793 Free PMC article.
References
-
- Murphy K, Travers P, Walport M (2007) Janeway’s Immunobiology (Immunobiology: The Immune System (Janeway)): Garland Science.
-
- Subramanian VG, Duffy KR, Turner ML, Hodgkin PD (2008) Determining the expected variability of immune responses using the cyton model. J Math Biol 56: 861–892. - PubMed
-
- Weston SA, Parish CR (1990) New fluorescent dyes for lymphocyte migration studies. Analysis by flow cytometry and fluorescence microscopy. J Immunol Methods 133: 87–97. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

