Bladder wall thickness mapping for magnetic resonance cystography
- PMID: 23835844
- PMCID: PMC3739434
- DOI: 10.1088/0031-9155/58/15/5173
Bladder wall thickness mapping for magnetic resonance cystography
Abstract
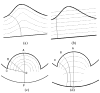
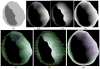
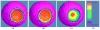
Clinical studies have shown evidence that the bladder wall thickness is an effective biomarker for bladder abnormalities. Clinical optical cystoscopy, the current gold standard, cannot show the wall thickness. The use of ultrasound by experts may generate some local thickness information, but the information is limited in field-of-view and is user dependent. Recent advances in magnetic resonance (MR) imaging technologies lead MR-based virtual cystoscopy or MR cystography toward a potential alternative to map the wall thickness for the entire bladder. From a high-resolution structural MR volumetric image of the abdomen, a reasonable segmentation of the inner and outer borders of the bladder wall can be achievable. Starting from here, this paper reviews the limitation of a previous distance field-based approach of measuring the thickness between the two borders and then provides a solution to overcome the limitation by an electric field-based strategy. In addition, this paper further investigates a surface-fitting strategy to minimize the discretization errors on the voxel-like borders and facilitate the thickness mapping on the three-dimensional patient-specific bladder model. The presented thickness calculation and mapping were tested on both phantom and human subject datasets. The results are preliminary but very promising with a noticeable improvement over the previous distance field-based approach.
Figures






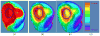


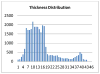
Similar articles
-
A coupled level set framework for bladder wall segmentation with application to MR cystography.IEEE Trans Med Imaging. 2010 Mar;29(3):903-15. doi: 10.1109/TMI.2009.2039756. IEEE Trans Med Imaging. 2010. PMID: 20199924 Free PMC article.
-
Quantitative Analysis of Bladder Wall Thickness for Magnetic Resonance Cystoscopy.IEEE Trans Biomed Eng. 2015 Oct;62(10):2402-9. doi: 10.1109/TBME.2015.2429612. Epub 2015 May 5. IEEE Trans Biomed Eng. 2015. PMID: 25955985
-
A unified EM approach to bladder wall segmentation with coupled level-set constraints.Med Image Anal. 2013 Dec;17(8):1192-205. doi: 10.1016/j.media.2013.08.002. Epub 2013 Aug 16. Med Image Anal. 2013. PMID: 24001932 Free PMC article.
-
Bladder tumors: virtual MR cystoscopy.Abdom Imaging. 2006 Jul-Aug;31(4):483-9. doi: 10.1007/s00261-005-0132-z. Abdom Imaging. 2006. PMID: 16568363 Review.
-
MR imaging of bladder diseases.Magn Reson Imaging Clin N Am. 1996 Aug;4(3):565-81. Magn Reson Imaging Clin N Am. 1996. PMID: 8873020 Review.
Cited by
-
Assessment of colon and bladder crosstalk in an experimental colitis model using contrast-enhanced magnetic resonance imaging.Neurogastroenterol Motil. 2015 Nov;27(11):1571-9. doi: 10.1111/nmo.12654. Epub 2015 Aug 24. Neurogastroenterol Motil. 2015. PMID: 26303228 Free PMC article.
-
Three-dimensional texture features from intensity and high-order derivative maps for the discrimination between bladder tumors and wall tissues via MRI.Int J Comput Assist Radiol Surg. 2017 Apr;12(4):645-656. doi: 10.1007/s11548-017-1522-8. Epub 2017 Jan 21. Int J Comput Assist Radiol Surg. 2017. PMID: 28110476
-
First performance evaluation of easyPET.3D, a high-resolution and cost-effective benchtop preclinical PET scanner.EJNMMI Phys. 2025 May 26;12(1):48. doi: 10.1186/s40658-025-00757-0. EJNMMI Phys. 2025. PMID: 40418258 Free PMC article.
-
α-Information-Based Registration of Dynamic Scans for Magnetic Resonance Cystography.IEEE J Biomed Health Inform. 2016 Jul;20(4):1160-70. doi: 10.1109/JBHI.2015.2441744. Epub 2015 Jun 17. IEEE J Biomed Health Inform. 2016. PMID: 26087506 Free PMC article.
-
Contrast enhanced magnetic resonance imaging as a diagnostic tool to assess bladder permeability and associated colon cross talk: preclinical studies in a rat model.J Urol. 2015 Apr;193(4):1394-400. doi: 10.1016/j.juro.2014.10.120. Epub 2014 Nov 14. J Urol. 2015. PMID: 25463988 Free PMC article.
References
-
- Siegel R, Naishadham D, Jemal A. Cancer statistics, 2013. A Cancer Journal for Clinicians. 2013;63:11–30. - PubMed
-
- Shaw ST, Poon SY, Wong ET. Routine urinalysis: Is the dipstick enough? The Journal of the American Medical Association. 1985;253:1596–1600. - PubMed
-
- Grossfeld GD, Carroll PR. Evaluation of asymptomatic microscopic hematuria. Urologic Clinics of North America. 1998;25:661–676. - PubMed
-
- Steiner GD, Trump DL, Cummings KB. Metastatic bladder cancer: Natural history, clinical course, and consideration for treatment. Urologic Clinics of North America. 1992;19:735–746. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
