Modelling Competing Endogenous RNA Networks
- PMID: 23840508
- PMCID: PMC3694070
- DOI: 10.1371/journal.pone.0066609
Modelling Competing Endogenous RNA Networks
Abstract
MicroRNAs (miRNAs) are small RNA molecules, about 22 nucleotide long, which post-transcriptionally regulate their target messenger RNAs (mRNAs). They accomplish key roles in gene regulatory networks, ranging from signaling pathways to tissue morphogenesis, and their aberrant behavior is often associated with the development of various diseases. Recently it has been experimentally shown that the way miRNAs interact with their targets can be described in terms of a titration mechanism. From a theoretical point of view titration mechanisms are characterized by threshold effect at near-equimolarity of the different chemical species, hypersensitivity of the system around the threshold, and cross-talk among targets. The latter characteristic has been lately identified as competing endogenous RNA (ceRNA) effect to mark those indirect interactions among targets of a common pool of miRNAs they are in competition for. Here we propose a stochastic model to analyze the equilibrium and out-of-equilibrium properties of a network of [Formula: see text] miRNAs interacting with [Formula: see text] mRNA targets. In particular we are able to describe in detail the peculiar equilibrium and non-equilibrium phenomena that the system displays in proximity to the threshold: (i) maximal cross-talk and correlation between targets, (ii) robustness of ceRNA effect with respect to the model's parameters and in particular to the catalyticity of the miRNA-mRNA interaction, and (iii) anomalous response-time to external perturbations.
Conflict of interest statement
Figures
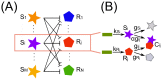
 ) and ceRNA (
) and ceRNA ( ) present in the network we consider the main steps of transcription (rates
) present in the network we consider the main steps of transcription (rates  and
and  respectively) and degradation (rates
respectively) and degradation (rates  and
and  respectively) plus a titrative interaction between miRNA and ceRNA. miRNA and ceRNA can therefore form a complex
respectively) plus a titrative interaction between miRNA and ceRNA. miRNA and ceRNA can therefore form a complex  with effective association rate
with effective association rate  . The parameter
. The parameter  (the catalyticity parameter) tells which is the probability a miRNA is recycled after having interacted with one of its targets.
(the catalyticity parameter) tells which is the probability a miRNA is recycled after having interacted with one of its targets.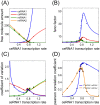
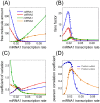

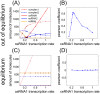
 . The threshold effect is possible only if the system is out of equilibrium (A). Numerical integration of Equation (1) in File S1 leads to time evolution of each molecular species for a given set of parameters. In panels A,C we plot "pictures" of the evolving system at different time
. The threshold effect is possible only if the system is out of equilibrium (A). Numerical integration of Equation (1) in File S1 leads to time evolution of each molecular species for a given set of parameters. In panels A,C we plot "pictures" of the evolving system at different time  (panel A
(panel A  , panel C
, panel C  ) as a function of ceRNA1 transcription rate. When t is smaller than the time complexes need to reach their steady state a threshold effect is observed. In panels B,D we plot the corresponding Pearson's coefficient profiles. Where the threshold effect is present (panel A), a peak in the Pearson's coefficient is also observed.
) as a function of ceRNA1 transcription rate. When t is smaller than the time complexes need to reach their steady state a threshold effect is observed. In panels B,D we plot the corresponding Pearson's coefficient profiles. Where the threshold effect is present (panel A), a peak in the Pearson's coefficient is also observed.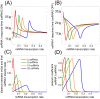
References
-
- Winter J, Jung S, Keller S, Gregory R, Diederichs S (2009) Many roads to maturity: microrna biogenesis pathways and their regulation. Nature cell biology 11: 228–34. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

