Systems approach to developmental biology--designs for robust patterning

Abstract

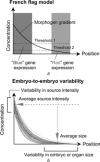
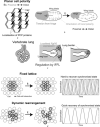
Patterning is an important step in animal development that generates spatially non-uniform gene expression patterns or spatially heterogeneous cellular responses. Patterning is realised by the generation and reading of positional information provided by spatial gradients of morphogens, diffusive chemicals in the extracellular environment. To achieve normal development, accurate patterning that is robust against noise is necessary. Here the authors describe how morphogen gradient formation and gradient interpretation processes are designed to achieve highly reproducible patterning. Furthermore, recent advancements in measurement and imaging techniques have enabled researchers to obtain quantitative dynamic and multi-physical data, not only for chemical events, but also for the geometrical and mechanical properties of cells in vivo. The authors briefly review some recent studies on the effects of such non-chemical events on patterning.

Fig. 1

Morphogen dependent patterning a French flag model. Thresholding responses to the concentration gradient of a morphogen can divide an embryo or organ into sub‐domains b Embryo‐to‐embryo variability of morphogen gradients. Variability in source intensity or embryo size is a typical noise source in patterning processes

Fig. 2

Different mechanisms for generating morphogen gradients a Three typical morphogen gradient profiles: linear, exponential and power‐law b Model equations for generating the three gradients. u (x, t) is the morphogen concentration at position x and at time t. D and γ are the diffusion constant and degradation rate, respectively. U _S is the intensity of morphogen source c Spatial profiles of the inverse of PP (i.e. ambiguity of positional information) (see the text for the definition of PP). Suppose that variability in source intensity is the main noise source and that the noise obeys Gaussian distribution, $N\left(U_{\mathrm{S}},{\sigma }_0^2\right)$. When σ ₀ is proportional to U _S, the value 1/PP (or PP) is independent of source intensity U _S and position x only for the exponential gradient. In contrast, PP of the linear gradient depends on x, and that of the power‐law gradient depends on both x and U _S d Definition of PP. PP is defined as the absolute value of the ratio of the gradient steepness (du /dx) to the magnitude of noise (σ (x)) at each position x

Fig. 3

Gradient scaling a The linear gradient by the source–sink model scales with embryo size b Expansion‐repression model. In this model, the second chemical, called the expander (denoted by E), facilitates the spread of the morphogen (denoted by M), which defines patterning, by enhancing its diffusion or protecting it from degradation. In turn, expander production is repressed by morphogen signalling. Scaling is achieved if the expander is stable and diffusible. In the equation, D and α are the diffusion constant and degradation rate, respectively. T _rep is the concentration of M which gives the half‐maximum synthesis rate of E. β_E is the maximum synthesis rate of E

Fig. 4

Information‐theoretical formulation of morphogen‐dependent positioning a Single‐morphogen case b Two‐morphogen case. By analogy to computer communication, a morphogen gradient can be regarded as a way of ‘encoding’ positional information: cells cannot directly recognise their positions. The positional information (i.e. spatial coordinate x) is transferred to cells after being converted into transmissive quantities, that is, morphogen concentrations. In this manner, a morphogen gradient provides a rule that relates the information that should be transferred (x) to the transmissive quantity (u ₁, u ₂, …). In noisy situations, cells located at each position x observe morphogen concentration $\left(u_1^{\prime },u_2^{\prime },\dots \right)$ with probability $P\left(u_1^{\prime },u_2^{\prime },\dots ;x\right)$. Cells have to estimate their true positions from the observed morphogen concentrations and respond appropriately according to the positions. Again by analogy to computer communications, this estimation process is regarded as a way of ‘decoding’ positional information. For a given observation, the likelihood of x, $L\left(x|u_1^{\prime },u_2^{\prime },\dots \right)$, can be calculated using $P\left(u_1^{\prime },u_2^{\prime },\dots ;x\right)$. The ML estimation gives the minimum mean square error c When the noises associated with two gradients are correlated, the precision can be improved if an appropriate combination of the sign of correlation and relative orientations of the morphogen gradients is chosen: for positive noise correlation, the precision is greater for oppositely‐directed gradients, and vice versa

Fig. 5

Different network motifs and their functions. pFBL (A–F), iFFL (G–J) and nFBL (K–M) a and b Thresholding and memory are two typical functions of pFBLs c Auto‐activation system d ASSURE‐type network e and f Bifurcation diagrams and examples of input–output curves for the auto‐activation and ASSURE networks, respectively g iFFL network motif h Typical input–output curve for an iFFL i Function of an iFFL as a single‐stripe generator j Position of a generated stripe becomes robust against the fluctuations of morphogen production at its source by combining an iFFL with a pFBL. See the text for details k Expression of segmentation genes (denoted by P) during vertebrate somitogenesis is regulated by an nFBL (specifically, auto‐regulation). The period of oscillatory expression determines the timing of segmentation l For appropriate levels of cell–cell interaction, oscillatory expression among cells is synchronised m For spatial gradients of parameter values for biochemical reactions in cells along the anterior‐posterior axis, a travelling wave can appear, through which the temporal oscillation pattern is converted into a spatially periodic pattern

Fig. 6

Recognition of relative position based on maximum likelihood (ML) decoding a Two exponential gradients in different embryos with different sizes b If the variation in embryo size is the dominant noise source, the correlation between the observed concentrations of the two morphogens $\left(u_1^{\prime },u_2^{\prime }\right)$ at each relative position y becomes very high (nearly equal to 1) c Cells located at y ₀ observe the set of morphogen concentrations $\left(u_1^{\prime },u_2^{\prime }\right)$ that distributes on curve C (y ₀), meaning that the ML estimate of position ${\hat{y}}_{\text{ML}}$ for the observation $\left(u_1^{\prime },u_2^{\prime }\right)\in C(y)$ is y. The following parameter values were used: (α ₁, α ₂) = (4, 5), (c ₁, c ₂) = (1, 1) and y ₀ = 0.34 d Best output function to minimise error in recognition of relative position y e (Top) 50 samples of gradient pairs (grey curves) and average profiles of morphogen gradients (black curves). There is no error in partitioning (dotted: output). (Bottom) Outputs for the 50 sample gradients for a single morphogen based on simple dose thresholding responses (thin black) f In a more general situation, the observed concentrations do not form a curved line but are elliptically distributed (black dots). However, the basic ideas for achieving region partitioning with the minimum error are similar to those in the above simple example

Fig. 7

Effects of cell/tissue geometry and mechanics on patterning a PCP, asymmetries within the plane of an epithelium (e.g. direction of hair). In each cell, PCP is generated by intercellular feedback signalling through PCP core molecules on cell membranes b In Drosophila wing formation, an anisotropic external force that is generated by hinge contraction acts on wing tissue. This force induces global and dynamic cell rearrangement, resulting in global orientation of PCP c During lung development, the localised expression pattern of Fgf10 depends on the geometry of the lung border d During somitogenesis, relative cell position dynamically rearranges through cell migration and/or cell division. Numerical simulations show that such a dynamic rearrangement promotes synchronisation of the segmentation clock, and for external perturbation, synchronisation is recovered much faster than in cases without cell movement