A century of enzyme kinetic analysis, 1913 to 2013
- PMID: 23850893
- PMCID: PMC4624389
- DOI: 10.1016/j.febslet.2013.07.012
A century of enzyme kinetic analysis, 1913 to 2013
Abstract
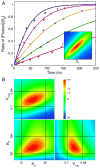
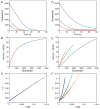
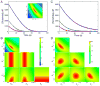
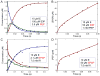
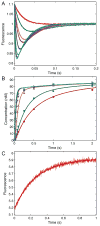
This review traces the history and logical progression of methods for quantitative analysis of enzyme kinetics from the 1913 Michaelis and Menten paper to the application of modern computational methods today. Following a brief review of methods for fitting steady state kinetic data, modern methods are highlighted for fitting full progress curve kinetics based upon numerical integration of rate equations, including a re-analysis of the original Michaelis-Menten full time course kinetic data. Finally, several illustrations of modern transient state kinetic methods of analysis are shown which enable the elucidation of reactions occurring at the active sites of enzymes in order to relate structure and function.
Keywords: 5-enoylpyruvoylshikimate-3-phosphate; 7-diethylamino-3-[([(2-maleimidyl)ethyl]amino)carbonyl]coumarin; Computer simulation; EPSP; Enzyme kinetics; Global data fitting; HIV reverse transciptase; HIVRT; MDCC; Michaelis–Menten; S3P; shikimate 3-phosphate.
Copyright © 2013 Federation of European Biochemical Societies. Published by Elsevier B.V. All rights reserved.
Conflict of interest statement
Figures



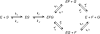


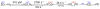
References
-
- Michaelis L, Menten ML. Die Kinetik der Invertinwirkung. Biochemische Zeitschrift. 1913;49:333–369.
-
- Goody RS, Johnson KA. The Kinetics of Inverase Action: translation of 1913 paper by Leonor Michaelis and Maud Menten. Biochemistry. 2011 http://pubs.acs.org/doi/suppl/10.1021/bi201284u. - DOI - PMC - PubMed
-
- Sainz-Polo MA, Ramirez-Escudero M, Lafraya A, Gonzalez B, Marin-Navarro J, Polaina J, Sanz-Aparicio J. Three-dimensional structure of Saccharomyces invertase: role of a non-catalytic domain in oligomerization and substrate specificity. The Journal of biological chemistry. 2013;288:9755–9766. - PMC - PubMed
-
- Henri V. Lois générales de l’action des diastases. Hermann; Paris: 1903.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

