Microstructural constitutive model of active coronary media

Abstract

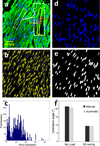
Although vascular smooth muscle cells (VSMCs) are pivotal in physiology and pathology, there is a lack of detailed morphological data on these cells. The objective of this study was to determine dimensions (width and length) and orientation of swine coronary VSMCs and to develop a microstructural constitutive model of active media. The dimensions, spatial aspect ratio and orientation angle of VSMCs measured at zero-stress state were found to follow continuous normal (or bimodal normal) distributions. The VSMCs aligned off circumferential direction of blood vessels with symmetrical polar angles 18.7° ± 10.9°, and the local VSMC deformation was affine with tissue-level deformation. A microstructure-based active constitutive model was developed to predict the biaxial vasoactivity of coronary media, based on experimental measurements of geometrical and deformation features of VSMCs. The results revealed that the axial active response of blood vessels is associated with multi-axial contraction as well as oblique VSMC arrangement. The present morphological database is essential for developing accurate structural models and is seminal for understanding the biomechanics of muscular vessels.

Keywords: Biaxial vasoactivity; Coronary artery; Deformation; Morphology; Vascular smooth muscle cell.

Figure 1

Experimental measurements of VSMC geometries. (a) Dimensions of a single VSMC, L_VSMC is the length and W_VSMC is the width; (b) Automatical measurement of VSMC orientations based on cell center-lines; (c) The histogram frequency distribution of VSMC orientations of a selected image. (d) The RGB image (Blue) of the cell nucleus; (e) Image processed by median filtering; (f) Comparison between manually and automatic measurements of VSMC orientation angle.

Figure 2

Distribution of VSMC geometrical parameters at ZSS. (a) Probability density functions (PDFs) of the lengths of VSMC and the nucleus; (b) PDFs of the widths of VSMC and the nucleus; (c) PDFs of the aspect ratios of VSMC and the nucleus; (d) PDFs of the orientation angles of VSMC and the nucleus. Columns present experimental measurements, and solid and dashed lines present normal distributions of geometrical parameters of VSMC and the nucleus, respectively.

Figure 3

The deformed VSMCs of coronary media under various distention pressures: The loading pressures in (a)-(e) are: 0 mmHg, 40 mmHg, 80 mmHg, 120 mmHg, 160 mmHg, respectively.

Figure 4

The nonlinear parameter-pressure relations of VSMC and the nucleus of coronary media. With the increase of distension pressure, (a) Changes of the length and with; (b) Change of the aspect ratio; (c) Measured and predicted changes of the orientation angle; (d) Measured and predicted VSMC and tissue deformation.

Figure 5

The second Piola-Kirchhoff total, passive and active stresses of coronary media. (a) The circumferential stresses at λ_z = 1.2; (b) The axial stresses at λ_z = 1.2; (c) The circumferential stresses at λ_z = 1.3; (d) The axial stresses at λ_z = 1.3. Symbols present experimental measurements, and solid lines present the predicted values from theory.