Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples
- PMID: 23874174
- PMCID: PMC3708855
- DOI: 10.1371/journal.pcbi.1003130
Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples
Abstract
Flow cytometry is the prototypical assay for multi-parameter single cell analysis, and is essential in vaccine and biomarker research for the enumeration of antigen-specific lymphocytes that are often found in extremely low frequencies (0.1% or less). Standard analysis of flow cytometry data relies on visual identification of cell subsets by experts, a process that is subjective and often difficult to reproduce. An alternative and more objective approach is the use of statistical models to identify cell subsets of interest in an automated fashion. Two specific challenges for automated analysis are to detect extremely low frequency event subsets without biasing the estimate by pre-processing enrichment, and the ability to align cell subsets across multiple data samples for comparative analysis. In this manuscript, we develop hierarchical modeling extensions to the Dirichlet Process Gaussian Mixture Model (DPGMM) approach we have previously described for cell subset identification, and show that the hierarchical DPGMM (HDPGMM) naturally generates an aligned data model that captures both commonalities and variations across multiple samples. HDPGMM also increases the sensitivity to extremely low frequency events by sharing information across multiple samples analyzed simultaneously. We validate the accuracy and reproducibility of HDPGMM estimates of antigen-specific T cells on clinically relevant reference peripheral blood mononuclear cell (PBMC) samples with known frequencies of antigen-specific T cells. These cell samples take advantage of retrovirally TCR-transduced T cells spiked into autologous PBMC samples to give a defined number of antigen-specific T cells detectable by HLA-peptide multimer binding. We provide open source software that can take advantage of both multiple processors and GPU-acceleration to perform the numerically-demanding computations. We show that hierarchical modeling is a useful probabilistic approach that can provide a consistent labeling of cell subsets and increase the sensitivity of rare event detection in the context of quantifying antigen-specific immune responses.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
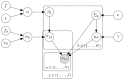
 event in the
event in the  sample is represented by
sample is represented by  , and the
, and the  component for the
component for the  sample is a multivariate Gaussian with proportion
sample is a multivariate Gaussian with proportion  , mean
, mean  and covariance matrix
and covariance matrix  .s. Hyper-parameters that can be set are
.s. Hyper-parameters that can be set are  ,
,  ,
,  ,
,  ,
,  and
and  as described in Methods. Given the declarative graphical model, standard and GPU-accelerated MCMC sampling algorithms can be used to implement the model as previously described .
as described in Methods. Given the declarative graphical model, standard and GPU-accelerated MCMC sampling algorithms can be used to implement the model as previously described .


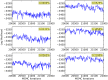



 ,
,
 ,
,
 and
and
 . To evaluate the robustness of the algorithm to changes in the configurable hyper-parameters, we repeated the analysis of the spiked in data sample multiple times with different parameters, using 10 independent MCMC runs to obtain statistics for each set of hyper-parameter configurations. Each mini-panel has the same axes as Figure 7 with estimated frequency of multimer-positive events on the vertical axis and spiked-in frequency on the horizontal axis. A boxplot is used to display the results for each model configuration. Configurable parameters were set to be either the default value (1.0), 3-fold lower (0.3) or 3-fold higher (3.0), giving 81 hyper-parameter configurations. Three replicate runs with 10,000 burn-in and 1,000 MCMC iterations were performed for each configuration. The default configuration is in the center panel with red text.
. To evaluate the robustness of the algorithm to changes in the configurable hyper-parameters, we repeated the analysis of the spiked in data sample multiple times with different parameters, using 10 independent MCMC runs to obtain statistics for each set of hyper-parameter configurations. Each mini-panel has the same axes as Figure 7 with estimated frequency of multimer-positive events on the vertical axis and spiked-in frequency on the horizontal axis. A boxplot is used to display the results for each model configuration. Configurable parameters were set to be either the default value (1.0), 3-fold lower (0.3) or 3-fold higher (3.0), giving 81 hyper-parameter configurations. Three replicate runs with 10,000 burn-in and 1,000 MCMC iterations were performed for each configuration. The default configuration is in the center panel with red text.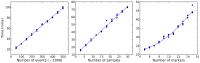
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

