Simplifying biochemical models with intermediate species
- PMID: 23883954
- PMCID: PMC3758008
- DOI: 10.1098/rsif.2013.0484
Simplifying biochemical models with intermediate species
Abstract
Mathematical models are increasingly being used to understand complex biochemical systems, to analyse experimental data and make predictions about unobserved quantities. However, we rarely know how robust our conclusions are with respect to the choice and uncertainties of the model. Using algebraic techniques, we study systematically the effects of intermediate, or transient, species in biochemical systems and provide a simple, yet rigorous mathematical classification of all models obtained from a core model by including intermediates. Main examples include enzymatic and post-translational modification systems, where intermediates often are considered insignificant and neglected in a model, or they are not included because we are unaware of their existence. All possible models obtained from the core model are classified into a finite number of classes. Each class is defined by a mathematically simple canonical model that characterizes crucial dynamical properties, such as mono- and multistationarity and stability of steady states, of all models in the class. We show that if the core model does not have conservation laws, then the introduction of intermediates does not change the steady-state concentrations of the species in the core model, after suitable matching of parameters. Importantly, our results provide guidelines to the modeller in choosing between models and in distinguishing their properties. Further, our work provides a formal way of comparing models that share a common skeleton.
Keywords: algebraic methods; model choice; multistationarity; stability; transient species.
Figures
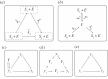
 ). (b) An extension model of network (a) with intermediate Y. (c) The complex y1 is involved in a reversible ‘dead-end’ reaction with one intermediate. (d) The complex y1 is converted into Y, which splits into y2 or y3, respectively (the former reversibly). (e) Schematic of (a).
). (b) An extension model of network (a) with intermediate Y. (c) The complex y1 is involved in a reversible ‘dead-end’ reaction with one intermediate. (d) The complex y1 is converted into Y, which splits into y2 or y3, respectively (the former reversibly). (e) Schematic of (a).
 . (b) Extension model. Conservation law curves (solid) as in (4.4) for different values of
. (b) Extension model. Conservation law curves (solid) as in (4.4) for different values of  and a3 = 2. (c) Extension model. Conservation law curves (solid) as in (4.4) for different values of a3 and
and a3 = 2. (c) Extension model. Conservation law curves (solid) as in (4.4) for different values of a3 and  . (Online version in colour.)
. (Online version in colour.)
Similar articles
-
Multistationarity in the Space of Total Concentrations for Systems that Admit a Monomial Parametrization.Bull Math Biol. 2019 Oct;81(10):4174-4209. doi: 10.1007/s11538-019-00639-4. Epub 2019 Jul 22. Bull Math Biol. 2019. PMID: 31332598
-
Addition of flow reactions preserving multistationarity and bistability.Math Biosci. 2020 Feb;320:108295. doi: 10.1016/j.mbs.2019.108295. Epub 2019 Dec 13. Math Biosci. 2020. PMID: 31843554
-
Multistationarity in Structured Reaction Networks.Bull Math Biol. 2019 May;81(5):1527-1581. doi: 10.1007/s11538-019-00572-6. Epub 2019 Feb 20. Bull Math Biol. 2019. PMID: 30788691
-
Mathematical and Statistical Techniques for Systems Medicine: The Wnt Signaling Pathway as a Case Study.Methods Mol Biol. 2016;1386:405-39. doi: 10.1007/978-1-4939-3283-2_18. Methods Mol Biol. 2016. PMID: 26677193 Review.
-
Systems biology and the origins of life? Part I. Are biochemical networks possible ancestors of living systems? Reproduction, identity and sensitivity to signals of biochemical networks.C R Biol. 2010 Nov-Dec;333(11-12):761-8. doi: 10.1016/j.crvi.2010.10.003. Epub 2010 Nov 17. C R Biol. 2010. PMID: 21146131 Review.
Cited by
-
Regulated bacterial interaction networks: A mathematical framework to describe competitive growth under inclusion of metabolite cross-feeding.PLoS Comput Biol. 2023 Aug 21;19(8):e1011402. doi: 10.1371/journal.pcbi.1011402. eCollection 2023 Aug. PLoS Comput Biol. 2023. PMID: 37603551 Free PMC article.
-
Regions of multistationarity in cascades of Goldbeter-Koshland loops.J Math Biol. 2019 Mar;78(4):1115-1145. doi: 10.1007/s00285-018-1304-0. Epub 2018 Nov 10. J Math Biol. 2019. PMID: 30415316
-
Connectivity of Parameter Regions of Multistationarity for Multisite Phosphorylation Networks.Bull Math Biol. 2024 Nov 4;86(12):144. doi: 10.1007/s11538-024-01368-z. Bull Math Biol. 2024. PMID: 39495318 Free PMC article.
-
The Inheritance of Local Bifurcations in Mass Action Networks.J Nonlinear Sci. 2025;35(4):72. doi: 10.1007/s00332-025-10165-4. Epub 2025 May 17. J Nonlinear Sci. 2025. PMID: 40390862 Free PMC article.
-
Oscillations and bistability in a model of ERK regulation.J Math Biol. 2019 Sep;79(4):1515-1549. doi: 10.1007/s00285-019-01402-y. Epub 2019 Jul 25. J Math Biol. 2019. PMID: 31346693
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

