Critical damping conditions for third order muscle models: implications for force control

Abstract

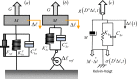
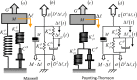
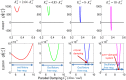
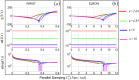
Experimental results presented in the literature suggest that humans use a position control strategy to indirectly control force rather than direct force control. Modeling the muscle-tendon system as a third-order linear model, we provide an explanation of why an indirect force control strategy is preferred. We analyzed a third-order muscle system and verified that it is required for a faithful representation of muscle-tendon mechanics, especially when investigating critical damping conditions. We provided numerical examples using biomechanical properties of muscles and tendons reported in the literature. We demonstrated that at maximum isotonic contraction, for muscle and tendon stiffness within physiologically compatible ranges, a third-order muscle-tendon system can be under-damped. Over-damping occurs for values of the damping coefficient included within a finite interval defined by two separate critical limits (such interval is a semi-infinite region in second-order models). An increase in damping beyond the larger critical value would lead the system to mechanical instability. We proved the existence of a theoretical threshold for the ratio between tendon and muscle stiffness above which critical damping can never be achieved; thus resulting in an oscillatory free response of the system, independently of the value of the damping. Under such condition, combined with high muscle activation, oscillation of the system can be compensated only by active control.

Fig. 1

Force control models of second-order mechanical systems. (a) Direct force control. (b) Indirect force control via position control. (c) Generalized impedance model of a second order mechanical system indicating the force fields that appear in the d'Alembert equation, Eq. (1).

Fig. 2

Third-order mechanical models of muscle-tendon systems. (a) Maxwell model (b) generalized impedance schematics of Maxwell model (c) Poynting-Thomson model (d) generalized impedance schematics of the PT model. (b) and (d) indicate the force fields that appear in the d'Alembert equation, Eq. (1). Each force field is a function of the mechanical paramenters of the elements that generate it.

Fig. 3

Discriminant of Poynting-Thomson model's characteristic polynomial shown as a function of muscle damping $C_{\theta }^P$ for four values of tendon/muscle stiffness ratio κ (2.64, 4.85, 8, 10). The function is shown for both wrist (top) and elbow (bottom). For κ < 8 the discriminant is positive, independent of the value of $C_{\theta }^P$, which translate in a free oscillatory response of the system. If κ ≥ 8 a finite interval of damping values exists within which the system does not present an oscillatory free response.

Fig. 4

Roots of Poynting-Thomson model's characteristic polynomial shown as functions of the damping $C_{\theta }^P$ for four values of tendon/muscle stiffness ratio κ (2.64, 4.85, 8, 10). The top row represents the real root; center and bottom rows represent the real and imaginary part of the two complex conjugate root, respectively.