Evoked centripetal Ca(2+) mobilization in cardiac Purkinje cells: insight from a model of three Ca(2+) release regions
- PMID: 23897231
- PMCID: PMC3779118
- DOI: 10.1113/jphysiol.2013.253583
Evoked centripetal Ca(2+) mobilization in cardiac Purkinje cells: insight from a model of three Ca(2+) release regions
Abstract
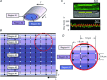
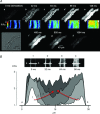
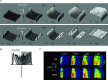
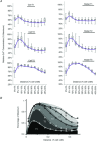
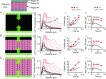
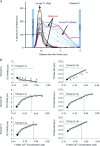
Despite strong suspicion that abnormal Ca(2+) handling in Purkinje cells (P-cells) is implicated in life-threatening forms of ventricular tachycardias, the mechanism underlying the Ca(2+) cycling of these cells under normal conditions is still unclear. There is mounting evidence that P-cells have a unique Ca(2+) handling system. Notably complex spontaneous Ca(2+) activity was previously recorded in canine P-cells and was explained by a mechanistic hypothesis involving a triple layered system of Ca(2+) release channels. Here we examined the validity of this hypothesis for the electrically evoked Ca(2+) transient which was shown, in the dog and rabbit, to occur progressively from the periphery to the interior of the cell. To do so, the hypothesis was incorporated in a model of intracellular Ca(2+) dynamics which was then used to reproduce numerically the Ca(2+) activity of P-cells under stimulated conditions. The modelling was thus performed through a 2D computational array that encompassed three distinct Ca(2+) release nodes arranged, respectively, into three consecutive adjacent regions. A system of partial differential equations (PDEs) expressed numerically the principal cellular functions that modulate the local cytosolic Ca(2+) concentration (Cai). The apparent node-to-node progression of elevated Cai was obtained by combining Ca(2+) diffusion and 'Ca(2+)-induced Ca(2+) release'. To provide the modelling with a reliable experimental reference, we first re-examined the Ca(2+) mobilization in swine stimulated P-cells by 2D confocal microscopy. As reported earlier for the dog and rabbit, a centripetal Ca(2+) transient was readily visible in 22 stimulated P-cells from six adult Yucatan swine hearts (pacing rate: 0.1 Hz; pulse duration: 25 ms, pulse amplitude: 10% above threshold; 1 mm Ca(2+); 35°C; pH 7.3). An accurate replication of the observed centripetal Ca(2+) propagation was generated by the model for four representative cell examples and confirmed by statistical comparisons of simulations against cell data. Selective inactivation of Ca(2+) release regions of the computational array showed that an intermediate layer of Ca(2+) release nodes with an ~30-40% lower Ca(2+) activation threshold was required to reproduce the phenomenon. Our computational analysis was therefore fully consistent with the activation of a triple layered system of Ca(2+) release channels as a mechanism of centripetal Ca(2+) signalling in P-cells. Moreover, the model clearly indicated that the intermediate Ca(2+) release layer with increased sensitivity for Ca(2+) plays an important role in the specific intracellular Ca(2+) mobilization of Purkinje fibres and could therefore be a relevant determinant of cardiac conduction.
Figures


Similar articles
-
Cardiac expression of ryanodine receptor subtype 3; a strategic component in the intracellular Ca2+ release system of Purkinje fibers in large mammalian heart.J Mol Cell Cardiol. 2017 Mar;104:31-42. doi: 10.1016/j.yjmcc.2017.01.011. Epub 2017 Jan 20. J Mol Cell Cardiol. 2017. PMID: 28111173
-
TRPM4 non-selective cation channels influence action potentials in rabbit Purkinje fibres.J Physiol. 2016 Jan 15;594(2):295-306. doi: 10.1113/JP271347. Epub 2015 Dec 14. J Physiol. 2016. PMID: 26548780 Free PMC article.
-
In situ Ca2+ dynamics of Purkinje fibers and its interconnection with subjacent ventricular myocytes.J Mol Cell Cardiol. 2005 Apr;38(4):561-9. doi: 10.1016/j.yjmcc.2005.01.004. J Mol Cell Cardiol. 2005. PMID: 15808833
-
The endoplasmic reticulum and junctional membrane communication during calcium signaling.Biochim Biophys Acta. 2013 Nov;1833(11):2542-59. doi: 10.1016/j.bbamcr.2013.06.004. Epub 2013 Jun 13. Biochim Biophys Acta. 2013. PMID: 23770047 Review.
-
NAADP receptors.Cold Spring Harb Perspect Biol. 2011 Jan 1;3(1):a004036. doi: 10.1101/cshperspect.a004036. Cold Spring Harb Perspect Biol. 2011. PMID: 21047915 Free PMC article. Review.
Cited by
-
Human Purkinje in silico model enables mechanistic investigations into automaticity and pro-arrhythmic abnormalities.J Mol Cell Cardiol. 2020 May;142:24-38. doi: 10.1016/j.yjmcc.2020.04.001. Epub 2020 Apr 3. J Mol Cell Cardiol. 2020. PMID: 32251669 Free PMC article.
-
Arrhythmia: 100 years on from George Ralph Mines.J Physiol. 2013 Sep 1;591(17):4065-6. doi: 10.1113/jphysiol.2013.262386. J Physiol. 2013. PMID: 24742770 Free PMC article. No abstract available.
-
Cardiac Purkinje fibers and arrhythmias; The GK Moe Award Lecture 2015.Heart Rhythm. 2016 May;13(5):1172-1181. doi: 10.1016/j.hrthm.2016.01.011. Epub 2016 Jan 13. Heart Rhythm. 2016. PMID: 26775142 Free PMC article.
-
Small caliber arterial endothelial cells calcium signals elicited by PAR2 are preserved from endothelial dysfunction.Pharmacol Res Perspect. 2015 Mar;3(2):e00112. doi: 10.1002/prp2.112. Pharmacol Res Perspect. 2015. PMID: 25729579 Free PMC article.
References
-
- Boittin FX, Coussin F, Macrez N, Mironneau C, Mironneau J. Inositol 1,4,5-trisphosphate- and ryanodine-sensitive Ca2+ release channel-dependent Ca2+ signalling in rat portal vein myocytes. Cell Calcium. 1998;23:303–311. - PubMed
-
- Bondarenko VE, Bett GC, Rasmusson RL. A model of graded calcium release and L-type Ca2+ channel inactivation in cardiac muscle. Am J Physiol Heart Circ Physiol. 2004;286:H1154–H1169. - PubMed
-
- Boyden PA, Albala A, Dresdner KP., Jr Electrophysiology and ultrastructure of canine subendocardial Purkinje cells isolated from control and 24-hour infarcted hearts. Circ Res. 1989;65(4):955–970. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

