Inverse Electrocardiographic Source Localization of Ischemia: An Optimization Framework and Finite Element Solution
- PMID: 23913980
- PMCID: PMC3727301
- DOI: 10.1016/j.jcp.2013.05.027
Inverse Electrocardiographic Source Localization of Ischemia: An Optimization Framework and Finite Element Solution
Abstract
With the goal of non-invasively localizing cardiac ischemic disease using body-surface potential recordings, we attempted to reconstruct the transmembrane potential (TMP) throughout the myocardium with the bidomain heart model. The task is an inverse source problem governed by partial differential equations (PDE). Our main contribution is solving the inverse problem within a PDE-constrained optimization framework that enables various physically-based constraints in both equality and inequality forms. We formulated the optimality conditions rigorously in the continuum before deriving finite element discretization, thereby making the optimization independent of discretization choice. Such a formulation was derived for the L2-norm Tikhonov regularization and the total variation minimization. The subsequent numerical optimization was fulfilled by a primal-dual interior-point method tailored to our problem's specific structure. Our simulations used realistic, fiber-included heart models consisting of up to 18,000 nodes, much finer than any inverse models previously reported. With synthetic ischemia data we localized ischemic regions with roughly a 10% false-negative rate or a 20% false-positive rate under conditions up to 5% input noise. With ischemia data measured from animal experiments, we reconstructed TMPs with roughly 0.9 correlation with the ground truth. While precisely estimating the TMP in general cases remains an open problem, our study shows the feasibility of reconstructing TMP during the ST interval as a means of ischemia localization.
Keywords: Bidomain Model; Electrocardiography; Finite Element Method; Inverse Problem; Myocardial Ischemia; PDE Optimization; Total Variation.
Figures

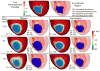



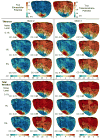

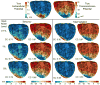
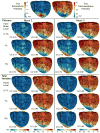
References
-
- SCIRun: A Scientific Computing Problem Solving Environment, Scientific Computing and Imaging Institute (SCI) 2011 Download from: http://www.scirun.org.
-
- Barr RC, Ramsey M, Spach MS. Relating epicardial to body surface potential distributions by means of transfer coefficients based on geometry measurements. IEEE Transactions on Biomedical Engineering. 1977;24(1):1–11. - PubMed
-
- Biros G, Ghattas O. Parallel Lagrange-Newton-Krylov-Schur methods for PDE-constrained optimization. Part I: The Krylov-Schur solver. SIAM Journal of Scientific Computing. 2005;27(2):687–713.
-
- Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
